CCF20120509086

M9L i^zęsc ii. Kozwiązama i oapowicuzi

skąd w wyniku całkowania otrzymamy:

dv ld p

T^{- =}    y + c i,

dy r] dx

(I)

, V 1 dp

^{y +C}>^J,+C2-

”00 = «77-

oraz dla y = 0 -> v = 0,
^1 H 2rj dx
H^2dpyf y\	(2)
2r]dxH\ HJ'
(I-h^A-zY	(3)
' H dx \2 H

Przy założonych warunkach brzegowych: dla y = H -> v = stałe całkowania wynoszą:

przeto

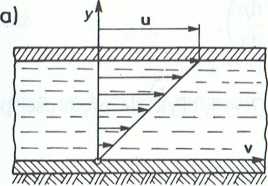
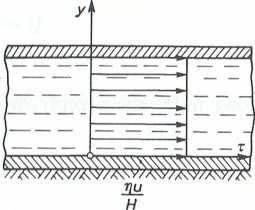
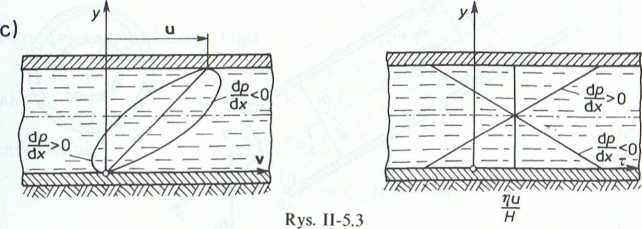
a.    Dla przepływu Couette’a (rys. II-5.3a)

u > 0,    = 0,

dx

u    , u

v(y) = ^x(y) = ^ = ^const •

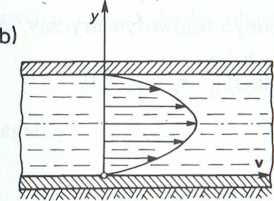
b.    W przypadku płaskiego przepływu Hagena-Poiseuille’a (rys. II-5.3b),

„ dp

u = 0,    < 0,

dx

W--2

H² dp y

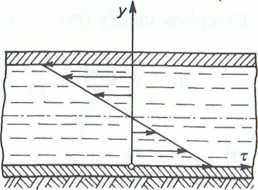
c. Dla ogólnego przypadku, w którym:

u > 0,    “ ^ 0,

QX

obowiązują zależności (2) i (3).

Profile (rozkłady) prędkości i naprężeń stycznych (w zależności od znaku gradientu i lśnienia) (rys. II-5.3c) są superpozycjami wariantów a i b. Należy przy tym podkreślić, '• naprężenie styczne w osi przepływu jest niezależne od gradientu ciśnienia i zanika w miejscu, gdzie prędkość osiągi wartość ekstremalną.

d. Objętościowe natężenie przepływu

Q = J»(y)di4,

A

yd/ie

dA = bdy

HI 11/

-^l

H2i, II \ H