CCF20120509�073
274 Część II. Kozwiązania i oopowieuzi
Ponieważ dla
t — 0, x — X{),
więc stała C — x05 zatem
x(t) = —v0t + x0.
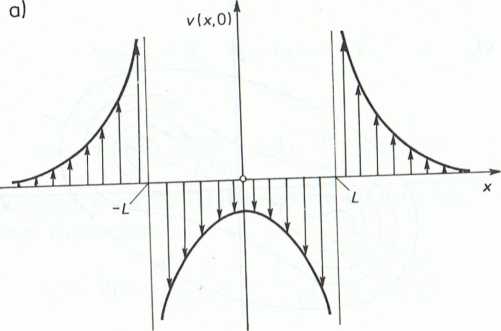
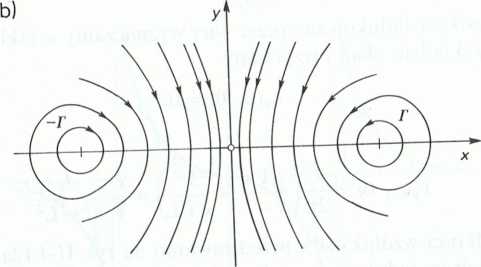
Rys. II-4.12
b. Prędkość v, otrzymana na skutek indukcji urojonej strugi wirowej rzeczywistą strugę 1 (rys. 11-4.13a), wynosi
r
l*o podstawieniu do powyższej zależności wyrażenia określającego x(t) otrzymamy
r i
v(t) = ---.
4tt — v0t + x0
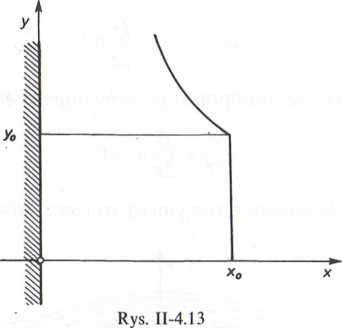
c. Struga wirowa porusza się po torze, którego asymptotą jest ściana (rys. II-4.13b). lej prędkość przy ścianie wzrasta do nieskończoności.
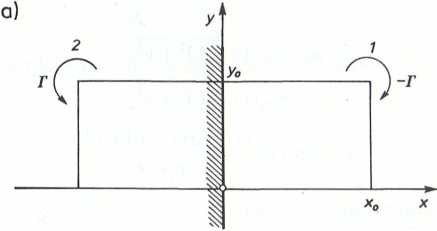
b)
1 4. Opływ ciał
4.4.1. Potencjał zespolony przepływu otrzymanego z superpozycji wynosi:
Q z + L
w(z) = u00z+—ln-(1)
271 z —L
|u/y czym
w (z) = (p(x,y) + 'ul/(x,y). (2)
Wyszukiwarka
Podobne podstrony:
CCF20120509�101 .1.14 Część II. Kozwiązama i odpowiedzi Ponieważ Ci =0, c2 = c orazŁ+3Ł + Ł+^). gdzi
CCF20120509�053 Z.IU Częsc li. Kozwiązania i oopowicuzi M = -M , zatem M = pQa>R2, a po podstawie
CCF20120509�037 IV<> Częsc II. Rozwiązania i odpowiedzi Po podstawieniu c = k/R i scałkowaniu
CCF20120509�065 częsc ii. Kozwiązania i oapimicu/.i Otrzymane tym sposobem wyrażenie jest równaniem
CCF20120509�088 306 Część II. Rozwiązania i odpowiedzi 5. Dynamika cieczy rzeczywistych 307 z któreg
287 jpeg ISBN 978-83-01.14*14-0. C l>> WN PWN 24HI7 274 CZĘŚĆ II Polityka handlowa zarówno w K
Część II Przemiany współczesnego piśmiennictwa dla najmłodszych GERTRUDA SKOTNICKA: Powieść
CCF20120509�032 IH<> Część II. Rozwiązania i odpowiedzi Objętościowe natężenie przepływu przez
CCF20120509�033 I HM Część II. Rozwiązania i odpowiedzi _ skąd po dodaniu stronami
CCF20120509�034 IW Część II. Rozwiązania i odpowiedzi stąd P = Pb P P kx2 kl -T+ 2X- a po przekształ
CCF20120509�035 192 Część II. Rozwiązania i odpowiedzi oraz 3xj "0P zależność (10) możemy zapis
CCF20120509�042 ZUO Część II. Rozwiązania i odpowiedzi 3.1.20. Prędkość wody wypływającej z otwarteg
CCF20120509�043 210 Część II. Rozwiązania i odpowiedzi /. rysunku II-3.7 wynika następująca zależnoś
CCF20120509�044 212 Część II. Rozwiązania i odpowiedzi 3.2.6. Natężenie wypływu przez elementarny pr
CCF20120509�046 216 Część II. Rozwiązania i odpowiedzi 216 Część II. Rozwiązania i odpowiedzi stąd R
CCF20120509�051 226 Część II. Rozwiązania i odpowiedzi wobec tego wzór (1) można przedstawić w nastę
CCF20120509�060 244 Część II. Rozwiązania i odpowiedzi b. Równania różniczkowe torów poruszania się
CCF20120509�062 ZSI) Częsc ll. Kozwiązama i odpowiedzi Spełnione jest również równanie ciągłości0X 0
CCF20120509�063 252 Częsc II. Rozwiązania i odpowiedzi Kierunek ruchu wyznaczymy przez określenie co
więcej podobnych podstron