CCF20120509053

Z.IU Częsc li. Kozwiązania i oopowicuzi

M = -M',

zatem

M = pQa>R²,

a po podstawieniu moment

pcoR²nd² r-— -ir—z

M ---yj 2gh + a)² R².

yj2 -9,81- 0,3 + (30)²(0,3)² = 1,98 N-m.

M =

Po wprowadzeniu wartości liczbowych moment reakcji 1000 ■ 30 • (0,3)²'3,14 • (0,01 )²

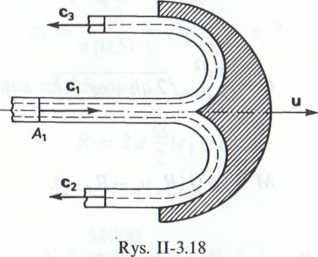
3.3.15. Strumienie masowe oraz poszczególne prędkości, odniesione do układu poruszającego się wraz z łopatką (oznaczone u góry kreską) wynoszą:

c[=c₁— u,    m'₁=pc[A_l,

C2 = c₂ + u,    m'₂ = pc'₂ A₂,

c₂ = c₃ + u,    m₃ = pc'₃ A₃.

Według zasady ilości ruchu reakcja hydrodynamiczna

R = m i ej — m^c^ —m 3C3.    (1)

Równanie (1) w układzie skalarnym przybierze następującą postać:

R = m\ cj —( — m'₂ ć₂ - m'₃ c'₃).    (2)

Jeżeli pominiemy bardzo małe odległości pomiędzy przekrojami 1-2 oraz 1-3 (rys. II-3.18) i uwzględnimy równość ciśnień, tj.:

Pl ~ P2 ~ P3 ~ Pb'

to z równań Bernoulliego wynika, że:

W /wii|/ku z powyższym z zależności (2) otrzymamy

R = c[ (m [ +m 2 + m 3).

/ równania ciągłości

m’₂ + m'₃ - m\; R = 2m\c\.

c\ = Cj — u

1'iinlowaź

mu/

rh\ - pc\ A_l = pA₁{c₁-u),

Hi iii reakcja hydrodynamiczna

R = 2 p A, (c₁ — u)².

\ U<>. Siła obciążająca rozpatrywany element rurociągu

R = (Pl-P2)^A + PQ(^C1~^C2)-

1'i'lllowilż

Cl = C₂ = c,

<.ili 111 /godnie z równaniem Bernoulliego

Pi = Pi = p;

*li|d

R = 0.

IMim ni działający na rozpatrywany rurociąg

M = r_i(pQc₁+p₁ A) + r₂(pQc₂ + p₂A).

Ml.i

r_i=r₂ = a, c_l = c₂ = c

mil/

Q = Ac

ii/i luniemy

M = 2 A a (pc² + p).

\ 1.17. Sl rumień cieczy dopływającej do wirnika jest pozbawiony zawirowań. 1 i ,    0. W związku z tym, wektor prędkości c, ma tylko składową promier