CCF20120509049

U.L Częsc II. Rozwiązania i odpowiedzi

a zatem z porównania zależności (7) i (8), współczynnik strat lokalnych, przy ostrej zmianie przekroju przepływowego z mniejszego na większy, wynosi:

U.L Częsc II. Rozwiązania i odpowiedzi

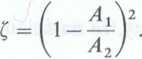
3.3.8. Na całej powierzchni rozpatrywanego strumienia wody panuje ciśnienie barometryczne p_b, wobec tego w równaniu równowagi pomijamy siły powierzchniowe, a-zatem

G + pQc₁ — pQc₂ = 0.

(1)

W przedstawionym wyrażeniu

c, = c,

Q = cA,

G= — pg V.

Prędkość c₂ wyznaczamy z równania Bernoulliego (przekroje 1 i 2):

Ź ₊ Pl ₊ o = $₊?1 ₊ H,

2 g pg    2 g pg

(2)

w którym stąd

Ci =c, p_x=p₂ = Pb;

c₂ = c² — 2gH.

Po podstawieniu określonych wielkości do wyrażenia (1) otrzymamy: — pgV+ pc² A — pAc^/c² — 2gH = 0,

(3)

wobec tego objętość strumienia

V=-{c-_yJc²-2gH).

g

3.3.9. Zgodnie z zasadą ilości ruchu wektor naporu hydrodynamicznego możemy określić za pomocą następującego równania:

R = m c, — m ec₂ — (1 — £)ńi c₃.    (1)

Z drugiej strony

R = R_v + R_v,

gdzie

R_x = m c_lx — m ec_2x — (1 — e)m c_2x = 0,

(2)

- R_y = mc_ly-m ec_2y - (1 - e)m c_3y.

(3)

Różnice wysokości pomiędzy poszczególnymi przekrojami, jako znikomo i pomijamy, a ciśnienie

Pi ~ P2 ~ P3 ~ Pb>

wobec tego

Ci — c₂ — c₃ — c.

Dla przyjętego układu osi współrzędnych (rys. 1-3.35), poszczególne skła< prędkości wynoszą:

clx = 0,	Cl, c,
^c2* = C,	^C2y =°>
= —csina,	c3), = — ccosa

/ulem równania (2) oraz (3) można przedstawić w następującej postaci:

R_x = — em c + (1 — e)m csina = 0,

— R_y= - mc + (l -s)m ccosa.

/ zależności (4) otrzymamy:

e

sina = --,

1 —£

./yli    s

a = arcsm--.

1 —e

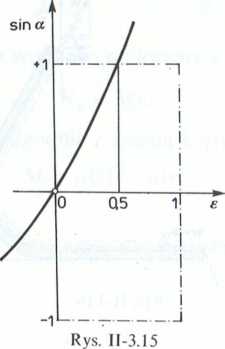
Na rysunku 11-3.15 przedstawiono funkcję sina = /(e), z której przebiegu wj • dla 1;    0,5, a = n/2 (zawsze e < 0,5). W takim przypadku, strumień odch

Hd/lt mini kierunek strumienia o prędkości c₂.