CCF20120509044

212 Część II. Rozwiązania i odpowiedzi

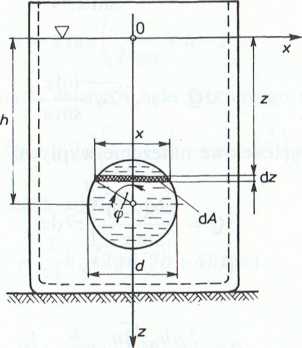
3.2.6. Natężenie wypływu przez elementarny przekrój d A (rys. II-3.9) wynosi:

d Q = ii_sJlgzxdz,

stąd

h + o

Q = Hy/2g xj~zdz.

h-

W układzie współrzędnych biegunowych:

x = dsincp,

, ^d

z = h—cos«>, 2

d z = -sincpdę,

wobec tego

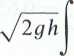
1---cosę sin²<pdę.

2 h

Q = ^d²

W celu scałkowania, wyraz /1--coscp rozwijamy w szereg potęgowy, przyjmując

\l 2/7

do rozwiązania jego trzy pierwsze wyrazy, a zatem:

1

'.ld \(d V ₂

'-22h^COS(P~ sUJ ^C°^S *

Rys. II-3.9

s'm²(pd(p.

Po scalkowaniu otrzymamy

q=

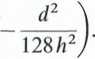
3.2.7. Zakładamy, że w każdym punkcie płaszczyzny otworu ciśnienie jest rów hydrostatycznemu, jak w zbiorniku lewym. W związku z tym, wysokość rozp rządzalna w całym otworze (dla wszystkich strumieni) jest jednakowa i wynosi:

H = (h + z) — z = h,

Uwzględniając prędkość dopływu c₀ i odpływu c_t, otrzymujemy wysokość rozp rządzalną

r² r¹

^H=^h+i⁺ł_g

()bjętościowe natężenie przepływu przez otwór jest równe:

Q = \iAj2gH.

Ponieważ

A =

kD²

zatem

Q

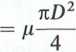
2 9

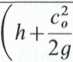
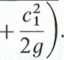
3.3. Reakcja strumienia cieczy.

Moment pędu (kręt)

3.3.1. Reakcja R (rys. II-3.10) w ruchu ustalonym strumienia cieczy wynosi:

^R = pCHc-Cj).

Natężenie przepływu Q oraz prędkość c_{ obliczamy z równania ciągłości: