CCF20120509035

192 Część II. Rozwiązania i odpowiedzi

oraz

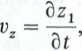
3xj

"0P zależność (10) możemy zapisać następująco:

Zi(ż\ +g) = -x₁ż\ lub

(11)

(12)

ż\(z₁+x₁) + z₁g = 0.

Z warunków zadania (A_t = 2A) wynika równość:

Zj +Xi = H,

stąd

Hż\ + gz_i = 0.

Całką ogólną równania różniczkowego (12) jest wyrażenie:

które po uwzględnieniu, że dla t = 0, z_t = H oraz ż_t = 0, przedstawia równanie ruchu powierzchni swobodnej cieczy w rurce pionowej, czyli:

Rozwiązując równanie (13) dla = 0, wyznaczymy czas t opróżniania rurki pionowej, a zatem:

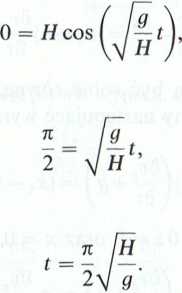
stąd

wobec tego

3.1.4. Układamy równanie Bernoulliego dla ruchu cieczy w dół (rys. 1-3.3):

Z warunku ciągłości przepływu stąd

c₂,

L , "i U i "2 «1 +— = «2 +—•

y y

Dla ruchu cieczy w górę otrzymamy:

^ci ,Pl,. C? P₂

— H---!-«! = — 4---h h₂,

y ¹ 2g y

gdzie

^ci ~ ^C2>

zatem

_Al+£i _{= A2 +} £2.

Z przeprowadzonej analizy wynika, że postać równania Bernoulliego dl; cieczy doskonałej w przewodzie pionowym nie zależy od kierunku przepływ

3.1.5. Dla przekroju 1 w zbiorniku i 2 na wypływie układamy równanie Ber

go:
•	c\ Pl , ^c2 P2 =- + — + * 1 =~^L + ~- y 2 g y
Ponieważ	Ci =0, hy = h2, Pl = p, Pz
przeto	P = Sl + ?£. y 2# y ’
stąd
	IMp - p„)

‘2-

3.1.6. Obieramy dwa przekroje: 1 — pod tłokiem oraz 2 — na wypływie (r; i układamy dla nich równanie Bernoulliego:

^ + — + 11 = -^ + — + 0.

2<y y    2g y

Prędkość c, wyznaczamy z równania ciągłości:

Q, =02,

13 — Mechanika płynów