CCF20120509063

252 Częsc II. Rozwiązania i odpowiedzi

Kierunek ruchu wyznaczymy przez określenie cosinusów kierunkowych wektora prędkości v o module równym:

v = y/vi + vf. = a_s/x² + y²,

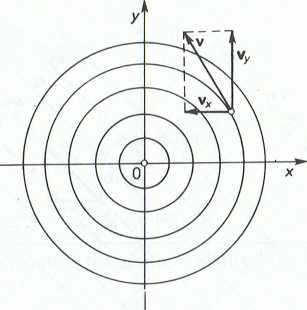
Rys. 11-4.4

wobec tego

cos(v,x)

y_x ~^ay

^v a_s/x² + y²

oraz

cos(v,y) = ^ = v

ax

aJx² + y²

4.1.11. Z zależności:

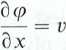
XI

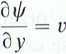
X1

otrzymamy

S i/z

0x ’

wobec tego funkcja prądu

<A =

dep

dx

dy-t-C^).

Różniczkując funkcję potencjału cp = C\njx² + y²,otrzymujemy

t)</> Cx 0x x² + y²’

l.)(l

iA = c

2, ₂dy + C,(x), x² +y²

i / vli

dl*

i\> = C

y²

' + ~2 x²

4" C! (x).

W związku z tym, funkcję prądu dla C, = O przedstawia następujące równanie:

\j/ = C aretg

y

1'inslc dane równaniem arc tg (y/x) = const lub we współrzędnych biegunowych, t/< - li = const, są rodziną linii prądu (rys. 11-4.5).

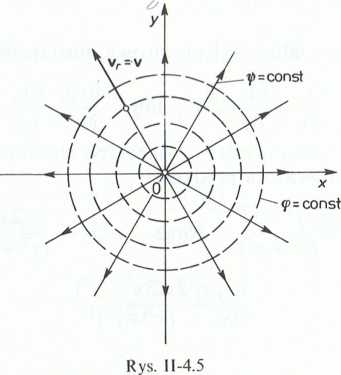
W celu wyznaczenia kierunku przepływu należy określić rolę, jaką spełnia znak 'iiilij (W tym celu korzystamy z układu współrzędnych biegunowych (r,.9), w którym

(p = C ln/%

l<i t• t«»

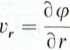
C

r

imliitniej zależności wynika, że dla C>0, prędkość przepływu skierowana jest i¹ < ul nie z kierunkiem promienia wodzącego i wówczas medium wypływa z początku mI ludu współrzędnych (źródła) wzdłuż linii prądu, będących promieniami.