CCF20120509032

IH<> Część II. Rozwiązania i odpowiedzi

Objętościowe natężenie przepływu przez dowolną powierzchnię A obliczamy z następującego wzoru:

e = R<u    (i3)

A

w którym v_n jest składową normalną wektora prędkości v w danym punkcie do powierzchni A.

W przepływie jednoparametrowym cieczy nieściśliwej

(14)

Q = cA,

przeto warunek ciągłości, przedstawiający równość objętościowych natężeń prze pływu, można wyrazić równaniem:

c_t A_y = c₂ A₂ = ... = const.    (15)

Dla masowego natężenia przepływu

m i = m ₂ = ... = const.    (16)

czyli

p Cj A_x = pc₂ A₂ = ... = const.    (17)

Reakcja R swobodnego strumienia płynu doskonałego jest równa naporowi hydrodynamicznemu P, z jakim strumień cieczy działa na przeszkodę znajdującą się w linii jego działania. Z zasady zachowania pędu

(IK)

d (m c) dt

W ruchu ustalonym reakcja strumienia

R = pG(Ci-c₂),    (lń)

gdzie pQ oznacza masę cieczy przepływającej w jednostce czasu, c, — średnią prędkość początkową, c₂ — średnią prędkość końcową.

Pochodna względem czasu wektora krętu

K = mc x r

układu materialnego, względem dowolnie obranego punktu, równa jest momentowi sil zewnętrznych układu względem tego punktu, czyli

dK d(mcxr)

_____    IV /■    .    > i i,

Przyrost krętu w czasie df będzie zatem równy momentowi reakcji hydrodynamiczni i wobec tego w ruchu ustalonym cieczy

< Mr/ymana zależność (równanie Eulera) dotyczy momentu względem osi obroti I)i zepływu osiowosymetrycznego.

ii. Zastosowanie równań hydrodynamicznych Eulera I równania Bernoulliego

.1.1.1. Składowe wypadkowej jednostkowej siły masowej wynoszą:

X = 0, Y= 0, Z = -g,

ii pochodne składowych prędkości (v_x = 2x, v_y = —2y i v_z = 0) są odpowit

równo

dt	= 0,	0X	= 2,	3vx ^ = 0, 3y	00, 0Z	= 0,
^dVy bt	= 0,	dvy 0x	= 0,	^=-2 0y	0tv 0Z	= 0,
dt	= 0,	dv, dx	= 0,	£=-0. 0 y	0U, 0Z	= 0.

W związku z tym, równania Eulera możemy przedstawić w następującej posU

dv_x    1 dp

^Vjc 0x    p3x’

5v_y _ _^3p

^Vy by    pdy’

0 =

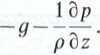
l'nil In winiąc dane oraz mnożąc obustronnie odpowiednie wyrażenia przez dx, ''O yiiinmy: