CCF20120509088

306

Część II. Rozwiązania i odpowiedzi

5. Dynamika cieczy rzeczywistych

307

z którego wynika, że dla r = 0

n2

v = v_m= —R ■ “ 4v

^ ₊ „.|!i ₊ ii^ ₊ ^,,_i_i8p _{+ v}('8^ ₊ I8S_£+I8X ₊ 8V

Elementarne objętościowe natężenie przepływu (rys. II-5.4b)

dQ =vdA,

^rSr r SS ~^z0z    p 0z ' ’\^0r²

l'o pominięciu siły masowej q_z i uwzględnieniu, że

0 V

v_z = v, v_r = v₉ = 0,    = 0,

ot

r 0r r² 0S²    0z²

S^

0Z

= 0,

gdzie:

dA = 2nrdr,

„ = ĄuW)_;

4v

stąd

Q =\vdA,

0

czyli

Q =

nJg

17

(R² — r²)rdr =

nJgR⁴

8v

możemy przedstawioną zależność sprowadzić do postaci równania różniczkowego zwyczajnego

r dr\ drj p 0z’

lub

klorego całką ogólną jest następujące wyrażenie:

Q =

nJgd⁴ 128 v

1

^dP..2

^{v =} ~a—~r~^r2 + Cj lnr + C₂. 4vp dz    ²

Prędkość średnia

Q

^{C =} A*

zatem dla

Z warunków brzegowych: Oraz

utrzymamy układ równań

dla	r = R„	O II
dla	r = R2,	v = 0,

A = nR²,

_ nJgR⁴ ₌

^C ~ 8vnR² 8v

Z wyprowadzonych zależności wynika, że prędkość średnia

1

^ 2^^max'

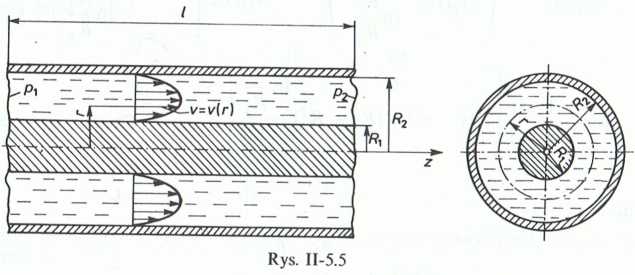
5 1 5 Podobnie jak w poprzednim przykładzie, rozwiążemy równanie Naviem -Stokesa dla przepływu w kierunku osi z (rys. II-5.5). W przyjętym układ/li współrzędnych cylindrycznych

1 dp

4vp dz

R% 4- Cj ln/?₂ + C₂ = 0,

/ których wyznaczamy stałe całkowania:

1 dpRj- Rf

4vp dz , R ’ ln—

Ri