CCF20120509096

322 Część II. Rozwiązania i odpowiedzi

a prędkość c_x, wyznaczona z warunku ciągłości

322 Część II. Rozwiązania i odpowiedzi

Cl

nDi

~T”

= c₂

n D\ 4 ’

wynosi

Cl

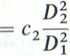
(2)

W związku z tym, z równania (1) wynika następująca zależność: 2g(H + Lsin a) =    1 +A^- + Cj-c|(^

a zatem

Ci —

2g(H + Lsina)

^{1 + A}K ^{+ C_}

Di

(3)

Zgodnie z warunkiem ciągłości, objętościowe natężenie przepływu cieczy doprowadzonej do zbiornika musi być równe ubytkowi płynu, czyli

Q = c₂

7tZ)i

4 ’

wobec tego

Q =

kD\ I 2g(H 4- Lsina)

5.2.5. W pierwszej kolejności obliczamy objętościowe natężenie przepływu

19600

<2 =

= 0,00585 m^J • s ,

930-3600

a następnie wyznaczamy prędkości średnie w części 1 i 2 przewodu, zatem

4 Q 4 0,00585

c, =

oraz

¹ nd\    3,14 (0,05)²

4 Q 4-0,00585

= 2,98 m-s"¹

ndl    3,14(0, l)²

= 0,745 m ■ s

-1

Liczby Reynoldsa dla poszczególnych odcinków rurociągu wynoszą:

c_ld_l 2,98-0,05

-6

Rej =

61 • 10

= 2443

oraz

= 1221.

_Re    ^c2^d2 0,745*0,1

^C2 v    61■10^-6

Ze wzoru Blasiusa obliczamy współczynniki strat na długości (współczynniki strat liniowych), zarówno dla węższej, jak i szerszej części przewodu.

Dla Rej > 2300,

,    0,3164    0,3164    _

¹ “ ^7r^ “ ^2443 “ ’    ’

n dla Re₂ < 2300,

64    64

/L = — = —- = 0,052. ² Re₂ 1221

Strata wysokości ciśnienia wywołana tarciem cieczy (strata na długości)

U

u — ii. 2 ii , ^C2 j ^l2 . ⁱ~2g^Ald₁⁺2g^A-²d₂'

Strata wysokości ciśnienia — miejscowa (lokalna) w rozszerzeniu przekroju

(c_l-c₂)² 2 g

,    (2,98 —0,745)² _n^_c

¹—2+sr~ " °-^{255 m}-

Całkowita strata wysokości ciśnienia

K = h_A +

r/.yli

h_s = 2,183 + 0,255 = 2,438 m, a .śpadek ciśnienia w przewodzie wyniesie

A p = pg

' r²—r² c2 ^C1

2 g

+ h , — h