CCF20120509037

IV<> Częsc II. Rozwiązania i odpowiedzi

Po podstawieniu c = k/R i scałkowaniu

P

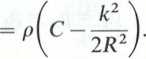
(2)

(3)

Dla R = R₀ i p = p_a stała całkowania przyjmie wartość

C = ^ + — p 2R²:

Po wstawieniu stałej C do równania (2) otrzymamy:

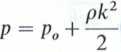
1

RŹ

(4)

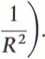
Z wyprowadzonej zależności wynika, że wraz z powiększającym się promieniem R, wzrasta ciśnienie cieczy p. (Równanie Bernoulliego obowiązuje dla danej linii prądu, zatem każda linia prądu ma swoją stałą C).

3.1.9. Prędkość wypływu cieczy obliczamy ze wzoru Torricellego, a zatem

C₂ = y/2 gH.

W celu wyznaczenia wysokości z₃ układamy równanie Bernoulliego dla przekroju

2 i 3:

c\ , Pi , „ cl p₃ + — + 0 = — + — + gz₃,

2 p    2 p

w którym c₃ = 0 oraz p₂ = p₃ = p_b\ stąd

ęl

2g

Ponieważ

c₂ = J2 gH,

wobec tego

z₃ = H.

Z przeprowadzonych rozważań wynika, że na wysokości z₃ = H, cała energia kinetyczna strumienia ulega ponownej przemianie w energię potencjalną.

3.1.10. Równanie Bernoulliego dla przekroju 1 względem 2 możemy zapisać następująco:

Wiedząc, że

C!»0, Pi=p_h, Zj — H + h, p₂ = P_b + pgh,

otrzymamy:

*+<<«+*)4₊E>±£!b.

P    2 p

skąd

c₂ = -JlgH-

Wykres przedstawiono na rys. II-3.3.

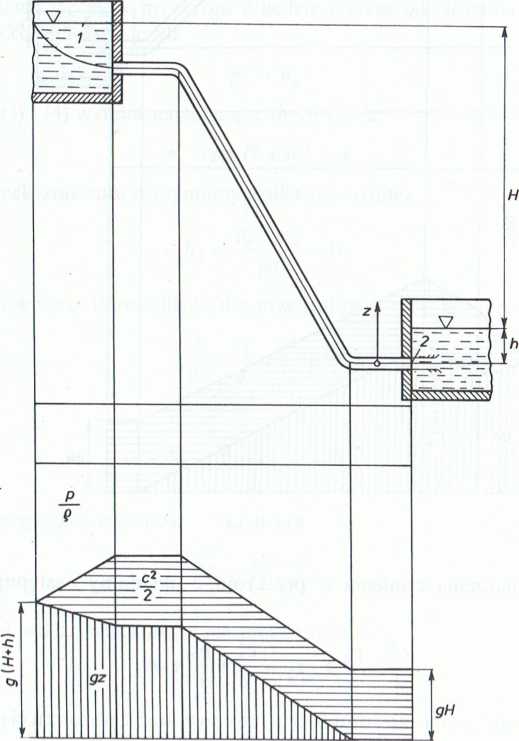
Rys. n-3.3