CCF20120509074

276 Część II. Rozwiązania i odpowiedzi

Z zależności

z = x + iy = r(cos$ + isin&)

i po przekształceniu odpowiednio wyrażenia (1) otrzymamy:

2n

27t r

w (z) = ę(x, y) + 'u]/(x, y) = (v_o0x + ^ln —) + i( t^y-^-3

gdzie

r_x = ^(x + L)² + y², r₂ = _s/(x — L)² + y²,

S = arccos

(x + L)(x — L) + y²

r.r

r 2

Wobec powyższego potencjał prędkości

(3)

, Q , r,

^{,p = v+}2i'"?;

oraz funkcja prądu

(4)

W celu określenia zerowej linii prądu przyrównujemy równanie (4) do zera, czyli

(5)

„„,-£9=0.

Z zależności (5) wynika, że liniami zerowymi są: oś rzeczywista oraz kontur tzw. owalu

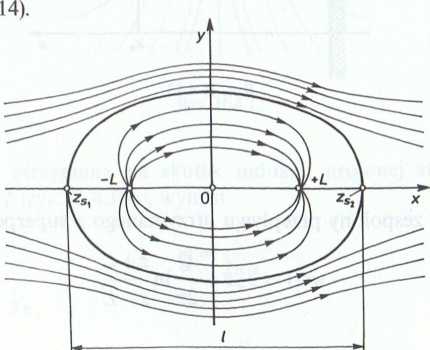
Rys. 11-4.14

Po przyrównaniu prędkości zespolonej do zera wyznaczymy położenie punktów spiętrzenia, a zatem

dw    LQ 1

d z

n z² — L²

= —--^ = 0,

skąd

z.,,= ±JL² +

QL

nv_r.

(6)

Punkty spiętrzenia leżą na osi rzeczywistej (rys. II-4.14), a długość owalu wynosi:

^l = ^zs₂-^=2lL² +

2. QL

nv_n

4.4.2. Potencjał zespolony

(1)

w(z) = vjz +

stąd

dw

LI

n z

^Vx-'^Vy = -^=^vJ ! + --)•

(2)

Ponieważ w punkcie spiętrzenia v_x = v = 0, przeto

(3)

(4)

^t,x-^v = ^oo( 1 + — - ) = 0, jr Zj

czyli

L

n

Współrzędna

z_s = x_s + iy_s

zatem

^zs = - - = x,-iy_s. n

Po przyrównaniu części rzeczywistej i urojonej otrzymamy współrzędne punktu spiętrzenia:

oraz y_s = 0.