CCF20120509102

w> Część II. Rozwiązania i odpowiedzi

Liczby Reynoldsa w poszczególnych przewodach wynoszą:

= 6400

oraz

cxd	25,6-0,01
V	0,4-10“^4
c2d	19,2-0,01
V	0,4-10“^4

wobec tego współczynniki strat na długości są odpowiednio równe:

,    0,3164    0,3164

A, = 4t== = ^7== = 0,035

yRe^" ^6400

oraz

₌ 0.038.

yse; yisoo

Suma wysokości strat w przewodzie tłocznym i spływowym

Cr + 2C& + Cd + Aj-j') +-^Z\ C_r +    + C_w + A₂-y ),

20

a po podstawieniu danych liczbowych:

4 + 2-0,25 + 1+0,035 ²

2-9,81

+

(19,2)²

0,01

4 + 2-0,25 + 0,5 + 0,038

0,01

2-9,81

Ciśnienie, jakie powinna wytworzyć pompa

P = Pi + pg^K

zatem

p = 7962000 + 900-9,81-725 = 14360000 Pa = 14,36 MPa. 5.3.5. Wysokość strat liniowych A h _x obliczamy ze wzoru Darcy’ego:

c² '/

^Ahx~2~g^k~d'

Po podstawieniu wartości liczbowych otrzymamy

u

= 725 m.

A/ij = . t „,0,03^ = 2,29c².

2-9,81    0,2

Równanie charakterystyki przewodu możemy przedstawić w następującej postni'

a po wstawieniu danych liczbowych

H = 20+ 10+ 2,29 c²,

czyli

H = 30 + 2,29c².

Ponieważ

c =

4Q

nd²’

ii więc

H = 30 + 2,29

16g²

n² (0,2)⁴ oraz po uproszczeniu

H = 30 + 2323 Q².

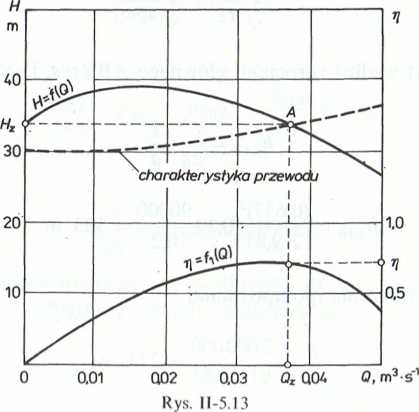
W celu sporządzenia charakterystyki przewodu, wyznaczamy z ostatniego równania wysokość H dla założonych wartości objętościowego natężenia przepływu Q. Wyniki zestawiono w tabeli:

Q m^3s-‘	0,00	0,01	0,02	0,03	0,04	0,05
H m	30	30,23	30,93	32,09	33,72	35,80

Otrzymaną w ten sposób krzywą nanosimy na wykres charakterystyki pompy (rys. II S.I3). Punkt A, przecięcia się dwóch krzywych, wyznacza objętościowe natężenie

Mocliunika płynów