CCF20120509065

częsc ii. Kozwiązania i oapimicu/.i

Otrzymane tym sposobem wyrażenie jest równaniem rodziny okręgów o promieniu r, których środki leżą w punktach (0, r) (rys. 11-4.6).

y

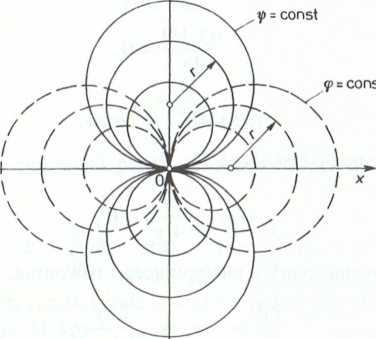
<p = const

Rys. 11-4.6

Linie ekwipotencjalne <p(x, y) = const jako ortogonalne do linii prądu i//(x, y) = const są również okręgami, których środki mają współrzędne (r, 0).

4.2. Ruch potencjalny płynu — zastosowanie rachunku zmiennej zespolonej

4.2.1. W pierwszej kolejności sprawdzamy, czy funkcja

<p{x,y) = C(x³ —3xy²)

może być potencjałem prędkości i spełnia równanie Laplace’a, zatem

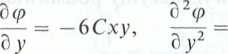
stąd

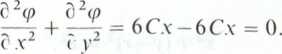
Uwzględniając zależność

0l/r _

0y ~    ⁼ 0 x’

4, Płaskie przepływy płynu doskonałego 257

0ę>

>tr/ymujemy

0iA

~ = 3C(x² —y²),

'Uld po scałkowaniu względem y

'l'(x,y) = 3 Cx²y-Cy³+/(x).

W wyrażeniu

3<A __    c (p

9* ^Vy~ ~ 9y ’

9<A    ć)tr>

g^ = ⁶ Cxy+j‘(x) oraz -^ = 6Cxy;

0y

'ii|d

/vll

6Cxy+/'(x) = 6Cxy, f’(x) = 0,

IM l 111

/(x) = C, = const.

" '^{wil,zku z} Powyższym, funkcję prądu możemy przedstawić w następującej postaci:

iA(x,y) = C(3x²y —y³) + Cj.

/ definicji potencjału zespolonego

w(z) = (p(x,y)+'n//(x,y),

" I"¹ podstawieniu znanych funkcji

(p(x,y) oraz    ij/(x,y),

= U(x³ — 3xy²) + i[C(3x²y — y³) + (',] =

^; Ux³ — 3 C.\y² + i C ■ 3 x²y — i Cr³ + i C, = C(x +iy)³ + iC,.

z = x + iy,

i"'•. ih |ii I zespolony wynosi:

w(z) = Cz³ + iC

¹ • lutnik u płynów