CCF20120509101

.1.14 Część II. Kozwiązama i odpowiedzi

Ponieważ

Ci =0, c₂ = c

oraz

Ł+³Ł + Ł+^).

gdzie

L= + /l₂ + /i + /2 + /I3 + /3,

Rys. II-5.12

czyli

stąd

L— 4 + 4 + 4 + 4+12 + 20 = 48

m;

H_z = h₂ + h₃ + h₄ + ^ + ^-(i + t;n + X_k + !;_d + ^).

Dla danych wartości liczbowych wysokość

„    ....    ¹⁰⁰⁰⁰⁰    (3,54)² /    48

= 4+12 + 2+.......+^rr( 1 + 5 + 3 ■ 0,3 + 1 +0,0147

1000-9,81    2-9,81

Moc silnika obliczamy z następującej zależności:

pgQH_z

N =

1000?? ’

0,06

40,76 m.

czyli

1000-9,81 -0,01 -40,76

1000-0,72    ’

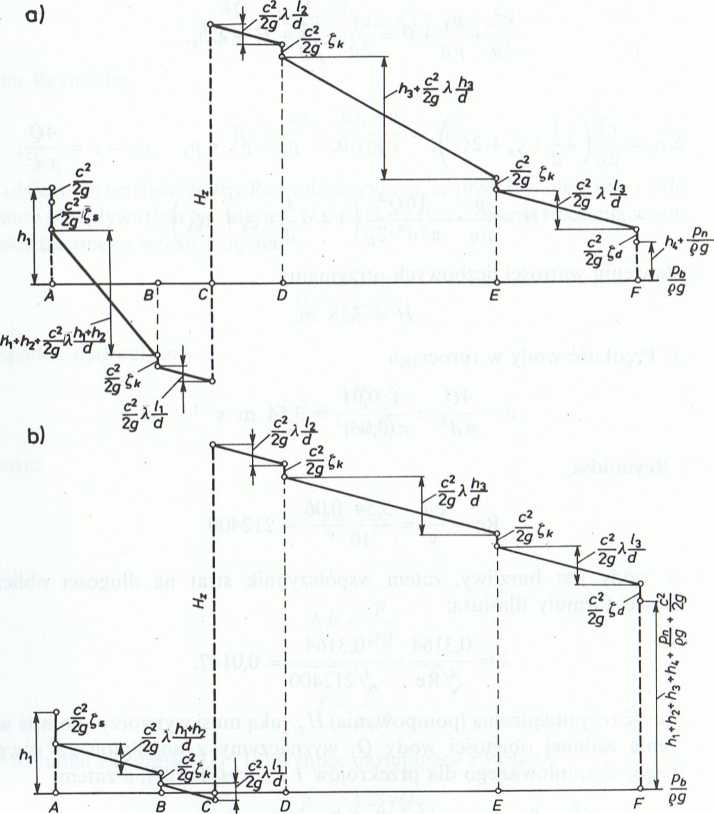
Wykresy: piezometryczny i zmian energii przedstawiono na rysunkach II-5.12a I 11-5.12b.

5.3.4. Ciśnienie p, działające na tłok 4P    4-160000

Pi =

nD² 7C (0,16)²

= 7962000 Pa = 7,962 MPa.

Prędkości cj i c₂, odpowiednio, w przewodzie tłocznym (/) oraz spływowym (2), wyznaczymy z równań ciągłości, a zatem:

71 d²

nD²

^ci~T~ = ^c—T 4    4

l + l

D²

' d²

- „ .(0.16)² ,,, ^=c^ ^{= 01}(aST)5 = ²⁵-^{6 m s}

iinalogicznie

nd² k ,    ,

c₂-T-= c-(D² - Dj),

i /yli

D²-D\

= 0,1

(0,16)² — (0,08)²

(0,01)²

= 19,2 m • s ¹.