CCF20120509�121

374 LZfSC ii. Kozwiązama i oupowicuzi
a wysokość rozporządzalna, wywołująca ruch cieczy w przewodzie
z = =- + 2 h„, 2(7
czyli
c2 c2
lub
(3)
z"^(i+c+Cz+Cd+4j-
Wyznaczając z równania (1) dh oraz ze wzoru (3) prędkość c i podstawiając je do zależności (2), otrzymujemy:
7iDj
4 1 +
Di
Dl
d z =
7td2
skąd
dt = —■
d i. -z 2dz.
Hl>v^
Po scałkowaniu otrzymanego równania w granicach od hj do /i2 otrzymamy czas częściowego opróżnienia zbiornika /ł:
t =
2DlJ\ +Cw + Cz + Cd + 2.^ / ‘ *
6.3. Uderzenie hydrauliczne
6.3.1. Prędkość rozchodzenia się fali uderzeniowej
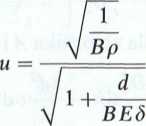
czyli
1+-
= 1160 m-s
-1
zatem przyrost ciśnienia
Ap = puca,
a więc
A p= 1000-1160 - 3 = 3480000 Pa = 3,48 MPa. 6.3.2. Prędkość rozchodzenia się fali uderzeniowej
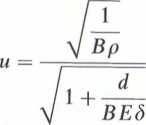
czyli
u =
1
8-10“3-800
0,276
= 1157 m-s-1,
10
10-10-2,06-104 • 10 • 10—3
a średnia prędkość przepływającego paliwa, przy pełnym otwarciu zaworu,
4 Q 4-0,17
Co = = 2’84 1X1 ‘ S '
na 7t (0,276)^
Przyrost ciśnienia obliczamy ze wzoru Żukowskiego:
A P = puc-,
gdzie
21 2-1000
t= — =. -- = 1,73 s, u 1157
a zatem
Ap — 800 1157-2,84• = 454765 Pa w 0,45 MPa.
Wyszukiwarka
Podobne podstrony:
CCF20120509�076 AOU Lzęsc ii. Kozwią/.ania i oupowicuzi l*o przyrównaniu części rzeczywistych i uroj
CCF20120509�040 LWL t^zęsc 11. Kozwiązama i oupowieuzi a po uproszczeniuyi(h-yi) = y2(h-y2)- Uzyskan
CCF20120509�073 274 Część II. Kozwiązania i oopowieuzi Ponieważ dla t — 0, x — X{), więc stała C — x
CCF20120509�075 t/rt v zęsc ii. Kozwiązama i oapowicuzi Na podstawie równania (2) możemy określić pr
CCF20120509�086 M9L i^zęsc ii. Kozwiązama i oapowicuzi skąd w wyniku całkowania otrzymamy: dv ld p T
CCF20120509�087 JU4 tzęsc ii. Kozwiązania i uapowicu/i 5. Dynamika cieczy rzeczywistych 305 stąd 1 d
CCF20120509�101 .1.14 Część II. Kozwiązama i odpowiedzi Ponieważ Ci =0, c2 = c orazŁ+3Ł + Ł+^). gdzi
CCF20120509�119 jw tzęsc ii. Rozwiązania i oupowicu/i jw tzęsc ii. Rozwiązania i oupowicu/i (1) (2)d
CCF20120509�120 ML Uzęsc li. Kozwiązania i oupowieuzi ML Uzęsc li. Kozwiązania i oupowieuzi (3) A(z)
CCF20120509�036 v,/,ęsc ii. i*uzwiązania i oupowicuzi oraz żalem Qi = nD2 ud2 Qi. — ~ę~c2> ctD2 =
CCF20120509�065 częsc ii. Kozwiązania i oapimicu/.i Otrzymane tym sposobem wyrażenie jest równaniem
CCF20100117�003 Dane do zadania projektowego nr8: Wysokość portalu H 2,5 [m] Rozstaw między stoja
CCF20110211�001 IUUJJUJJJJJJJJ I J J J J J J J J J J J J J J li J ii i: ii ii ii ii U ii
CCF20110228�005 (2) IiY-nu o ii o era ni. ćwiczeń hiboraroryj.nveh t chemii fizycznej. Liczby arabsk
CCF20110303�000 (9) "P *■»«—Łt/ ftjrSoj *4? <- “ / 1 ii . 1 ■ A# x7
CCF20110330�008 445K?! Uli •II;; • lijiwi-iiii h > ; > & ■ , 1 i il sowali przed sesją ko
CCF20110405�003 374 Magia, nauka i religia to ujawnia jej postać „animistyczna”, na którą kładł naci
CCF20111206�044 (Kopiowanie) R o /.dział II Jerzy KUNIKOWSKIPOZAMILITARNE UWARUNKOWANIA OBRONNE 1 i/
CCF20120509�032 IH<> Część II. Rozwiązania i odpowiedzi Objętościowe natężenie przepływu przez
więcej podobnych podstron