87737
Oznacza to, że tiapór cieczy na płaskie, poziome dno zbiornika jest równy iloczynowi ciśnienia hydrostaty cznego i pola powierzchni, przy czyni wypadkowa siła N tego napom jest oczywiście przyłożona w środku geometrycznym (środku ciężkości) powierzclmi F i skierowana pionowo w dół.
P*
V_i_i_i_i_i_i_i_i_
A

h
P
i
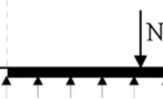
Rys.5.2. Napór cieczy na płaską poziomą powierzchnię.
W zależności 5.1 występuje iloczyn
V = F • h
będący objętością słupa cieczy o polu podstawy równym powierzclmi dna i wysokości równej głębokości zanurzenia powierzclmi, co pozwala przekształcić wz. (5.1) do postaci:
N = p • g • V (5.2)
która opisuje napór jako ciężar objętości V cieczy znajdującej się nad rozpatrywaną powierzchnią. Błędem byłoby jednak utożsamienie napom N z ciężarem cieczy znajdującej się w naczyniu, o czym przekonać może rys. 5.3 przedstawiający trzy różne zbiorniki o tym samym polu powierzchni dna i napełnione cieczą o gęstości p do tej samej wysokości li.
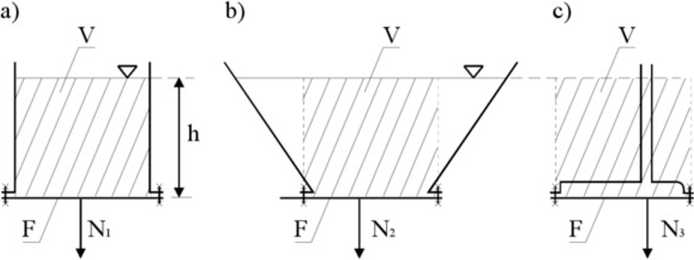
Rys.5.3. Paradoks Stevina dotyczący napom na dno zbiornika.
Mimo, iż w każdym ze zbiorników mieszczą się różne objętości cieczy, to napór na dno jest w każdym przypadku jednakowy, tzn.:
N, = N2 = Nj = p • g • h • F
Związek ten ilustruje paradoks Sterina o niezależności siły napom na dno naczynia od ilości cieczy■ zawartej w zbiorniku. Zależność (5.2) będzie natomiast poprawnie określać wielkość siły napom na dno, jeżeli przez V rozumieć będziemy objętość pozorną cieczy zawartej nad dnem określoną jako objętość słupa cieczy o polu podstawy równym powierzclmi dna i wysokości równej wysokości napełnienia zbiornika. Objętości pozorne cieczy zaznaczono na lys. 5.3 przez ich zakreskowanie, przy czym zauważyć można, że na rys. 5.3a objętość
89
Wyszukiwarka
Podobne podstrony:
CCF20111014�001 drut. Nie potrafi bowiem zmian przekształcających uznać za odwracalne. Oznacza to, ż
wadzenia w błąd słuchacza. Czy oznacza to że naruszamy wtedy maksymę jakości? A kiedy na przekór ocz
wadzenia w błąd słuchacza. Czy oznacza to że naruszamy wtedy maksymę jakości? A kiedy na przekór ocz
10575 ScannedImage 27 legionów na Wschodzie. Oznaczało to, że najwyższa władza nad Azją Mniejszą i E
TICGazy osłonowe □ Argon (Ar) jest gazem obojętnym. Oznacza to, że nie ulega utlenianiu i nie ma wpł
W sieci tego typu wszystkie komputery mogą się ze sobą komunikować na tych samych zasadach. Oznacza
Na wyższych uczelniach w Polsce dominuje następstwo pokoleń. Oznacza to, że pewne obszary badań, pew
1. Poziom ufności wynosi 0,95.Oznacza to, że parametr sigma: -nie znajdzie się w o
Addytywność cyrkulacji Oznacza to, że gdybyśmy powierzchnię ograniczoną konturem C podzielili na
Czas wojny rozgrywają się będąc na Polach wyrzucisz 2 oczka podczas ruchu, oznacza to, że
58 59 (15) 53 I. Spostrzega:# i niebieskoczułe. Oczywiście nie oznacza to, ze czopki są wrażliwe tyl
048 049 jesn w danym wierszu występuje (w polu kolumny Metoda) słowo Dane. oznacza to. że na wykresi
więcej podobnych podstron