3289580824

346 Dział czwarty. — Wytrzymałość uiateryaływ.

w punkcie ciężkości końcowego przekroju pręta prostego i w kierunku jego osi, oznaczymy przez:

l w cm długość pręta pracującego na wyboczcnic,

J w cm⁴ najmniejszy, równikowy moment bezwładności w najniebezpieczniejszym przekroju a (rys. 200 do 203), jE w kg/cm² spółczynnik sprężystości danego materyalu (patrz str.

331, 333 i nast).

L. Euler podał, stosownie do sposobu osadzenia komy pręta, poniższe wzory na:

Obciążenie wybaczające I\ w kg, gdy

Rys. 203.

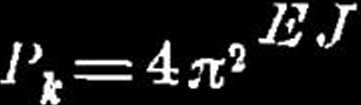
Rys. 200.

1) Jedoń koniec osadzony, drugi swobodny :

Rvs. 201.

2) Oby-

dwa końce swobodne, lecz prowadzone po osi pierwotnej A B\

Rys. 202.

3) Jeden koniec osadzo-

ny, drugi swobodny, lecz prowadzony po osi pierwotnej Ali:

Tl" EJ

Podług doświadczeń J. Bauschinger’a ¹) wielkości są obciążeniami krańcowemi, wybaczającemi, t. zn., że przy nieznacznem nawet powiększeniu tego obciążenia, wyboczenie pręta następuje nagle i dochodzi odrazu do bardzo znacznych rozmiarów.

2. Obciążenie bezpieczne pręta pracującego na wyboczenie będzie tylko:

P=P_k:<5,

przyczem <3 oznacza stopień bezpieczeństwa przeciw wyboczcniu, jaki stosujemy w danym przypadku.

Pręt o najmniejszym przekroju F cm², z materyalu, dla którego ciśnienie bezpieczne jest k kg/cm³, znosi obciążenie bezpieczne:

P₀ = k- F (kg).

Początkową długość wyboczenia /₀ otrzymamy, równając P i Po z wzorów powyższych, z uwzględnieniem sposobu osadzenia pręta przy wyborze jednego z 4-ch wzorów aa P. Otrzymana z równania tego długość /₀, oznacza tę długość pręta, prz}^T której będzie on równo wytrzymały aa ciśnienie proste jak i na wyboczenie. Nośność prętów krótszych niż l₀ oblicza się zatem wyłącznie na ciśnienie proste (P„), a prętów dłuższych wyłącznie na wyboczenie (/^ł).

1

Centralki, d. Rauvenv. 1880. str. 353 i nast.