3784490430

142

Z. Garczarczyk

gdzie dla równań (l) 1 (2) x £ Rⁿ jest nieznanym wektorem potencjałów węzłowych lub wektorem prędów i napięć rezystorów nieliniowych, u,i,v -wektory napięć i prędów gałęziowych oraz potencjałów węzłowych, h(u,l) -równania gałęziowe, g(*}# f(•) sę wektorami charakterystyk elementów nieliniowych, a pozostałe wielkości reprezentuję strukturę obwodu 1 źródła wymuszajęce [2], £3].

Skuteczne rozwlęzanie równań (l) - (3) wybranę metodę lteracyjnę więżę się z wyborem punktu startowego Wykorzystanie idei metody kontynuacji daje systematyczna metodę wyboru punktu startowego. W metodzie kontynuacji zamiast funkcji F(x)tO—>*Rⁿ, gdzie D c Rⁿ, rozważa się szczególna funkcję H(x,t) :D x T —Rⁿ, gdzie T »{t | Ośtśl} , zwanę homotopię, tzn.

h(x(t) ,t) * o,    x e o,    t e t

(4)

H (x ,0) - E (x) ,    h(x,1) « F(x) Vx 6 D

przy tym rozwlęzaniu x° ■ x(o) równania e(x) * 0 będęce punktem startowym jest znane lub łatwo Je uzyskać.

Rozwięzanla x(t) wyznaczane dla t rosnęcego tworzę ścieżkę (krzy-wę) w przestrzeni Rⁿ łęczęcę punkt x(0) z poszukiwanym rozwlęzaniem x^# a x(1) równania (l) - (3) [Y].

Istnieję różne sposoby konstruowania odwzorowania H(x,t) dla danego równania F(x) ■ O (por. [*4"], ^5]). Z twierdzenia o funkcji uwikłanej [l] wynika, że ścieżka homotopll istnieje, jeśli odwzorowanie H Jest regularne, tzn. macierz Oacobiego DH(x,t) ma maksymalny rzęd dla każdego (x,t) 6 h”¹, gdzie H“* » {(x,t) | H(x,t) ■ 0} oznacza zbiór wszystkich rozwlęzań (x,t) e Rⁿ układu (4). ścieżkę homotopll łęczęcę wy-brany punkt poczętkowy x° z punktem końcowym x a x(l) można wyznaczać punkt po punkcie przyjmujęc clęgłe lub dyskretne zmiany parametru t. Poszukujęc rozwięzanla równania f(x) * 0 dężymy przede wszystkim do uzyskania punktu x(l) możliwie jak najszybciej, nie zależy nam natomiast na dokładnym wyznaczaniu ścieżki homotopll. Zakładajęc dyskretne zmiany parametru t przyjmuje się pewien podział odcinka Ts

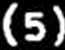
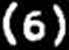
⁰ - ^to^{<    < l}N ■ ¹

i poszukuje się rozwlęzań równań

H(x,t_k) « O, k - 1,2,...N

lokalnie zbieżnę metodę lteracyjnę (na ogół metodę Newtona) przyjmujęc pewne przybliżenie poczętkowe x° (t^). To przybliżenie poczętkowe Jest