9346692693

Test ciągów sprawdza czy liczba nieprzerwanych ciągów zer i jedynek różnych długości w sekwencji s jest taka jakiej oczekujemy w sekwencji losowej. Oczekiwana ilość przerw⁷ i bloków⁸ długości i w n-bitowej sekwencji jest

n — i + 3 ⁶ⁱ ~ 2ⁱ⁺²

Niech k będzie równe największej liczbie całkowitej i, dla której e* ^ 5. Bi i Gi to ilości odpowiednio bloków i przerw o długości i G [1, k]. Używamy statystyki

T₄ = EfciL _{+ E}

(Gi-ei)

(4)

która spełnia rozkład x² o 2fc - 2 stopniach swobody.

Test autokorelacji. Celem tego testu jest sprawdzenie, czy nie występują korelacje pomiędzy wyrazami ciągu s i tym samym, ale przesuniętym ciągiem. Ustalmy d jako liczbę całkowitą taką, że 1 < d < \n/2\. Ilość bitów s różnych od ich odpowiedników w s przesuniętym o d bitów jest równa ^^Tg^d-1 si ® ^si+d-Używamy statystyki

T₅ = 2

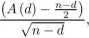
(5)

która jest zbliżona do rozkładu normalnego jeśli tylko n — d > 10. Ze względu na małe wartości A(d) są tak samo mało prawdopodobne jak duże, powinno się stosować testy dwustronne.

Test 7r polega praktycznie na zastosowaniu metody Monte Carlo do wyliczenia liczby 7r. Robi się to w ten sposób, że w kwadrat od długości boku 2a wpisuje się koło o promieniu a. Losując za pomocą generatora punkty w obszarze kwadratu sprawdzamy czy są one wewnątrz koła (ich liczbę oznaczmy przez k) to wtedy: gdzie n jest całkowitą liczbą losowanych punktów. Jak łatwo można zauważyć z równania (6): n = 4k/n, stąd też nazwa testu. Poniżej znajduje się wykres ilustrujący jak go spełniają generatory opisane w [4]:

2.3 Zestaw testów FIPS 140-1

Standard FIPS 140-1 określa cztery testy statystyczne losowości. Testy te nie wymagają od użytkownika podania poziomu istotności, w zamian dostarczają granic, w których powinny mieścić się obliczone statystyki. Każdemu z testów poddawany jest ciąg s o długości 20000 bitów. Jeśli którykolwiek z testów się nie powiedzie, generator nie przetrwa próby.

Ciągi zer. Ciągi jedynek.