4382790169

/*,»<* (I). Rodzi!U w*zynkich‘g((/) je* pobyciem otwntyra .raj „ będek rozkładem jedoofc, podporz*lkowuny_m pokryfcm Jeżeli * * 0 wSfA «o pcn.ev.ne s jen 1-1 ranny (o /) o g . 0 poza U. Dlatego równanie    ¹

f ⁹ f ^m f [l* f) ef)' MctJt’1

«to    v

nożna zapisać w ponaci

/ 9-f-f((*•/)•*]-IM/I. »u) i

Sl*

f ^fmHf * /^-53/((«> •/>«*) i<fe*f'ł =

*»    ^r«v-»

■ 53/<*°»></og>ld«ł'l- y</oj) łdetf^

t wagu. Twierdzenie to wynika ukzc z utozema. ż*

//= I </o*> !d«_t'|

*    /-(V)    ^

dla wazyMkkfc V * pewnego dopuazczalnego pokrycia zbioru g{A). Wynika lo z (|) zastosowanego do g *.

(2)    Wystarczy dowieś twierdzenia dla funkcp / ml.

Dowód (2). iezeii twierdzeń* zachodzi dla / - 1. lo zachodzi dla funkcji stałych. Niech V będzie przedziałem w g(A), a P — podziałem lego przedziału Dla każdego podpł/rdzułu S podziału P określmy /j jako funkcję rńwng «j(/). Wówczas

:/*-? / «*    * r'«atn

•

</*oj) ldetg'15

U/.P) = Tmsif) v(S>-

* !

i 53 ^ </«•»> We*g'l< J t/og}'\ó*g’[.

^S t-imn    ł *(V)

fkmiewaz f_v / fest kresem górnym wszystkich J.(J. P). dowodzi lo. te f_r f 2 /, -<vł</«>*) Ktołg'|. Podobno rozumowań*, przy pódiUwseniu /j - Mj(/) wykazuje. ** Jv i t f_r>_ir)(f°S) ■ Idei g'| Teza wynika teraz z tamknzcMinej powyżej uwagi.

(3)    Jeżeli twierdzenie jcsl prawdziwe dla g. A -* R* i dla h: B • R'- gdzie g(A) C B. lo jen ono prawdziwe dla hog: A » R\

tsfszzssa. ~j .

DowM O).

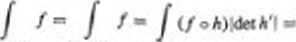
»U(A)I «M|

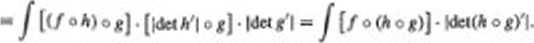
*    Ą

(4) Twierdzenie jest prawdziwe, jeżeli g jcM przekształceniem liniowym

Dowód (4). Na mocy < 1) i (2) wystarczy pokazać dla dowolnego przedziału otwartego

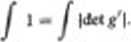
IW) V

U. i*

Jcu to zadanie 3.33

Wziąwszy razem punkty (3) i (4). widzimy, ze dla dowolnego utulonego a c A możemy założyć, że g'(a) jest nuestrzę jednostkowy: w istocie. jeśli T jest odwzorowaniem liniowym Ona). to (7"¹ o gYia) = /: ponieważ. twierdzenie jest prawdziwe dla r. więc yeżdi jest ono prawdziwe dla T"^x og, to jest też prawdziwe dla g.

Przygotowaliśmy już wszystko do podania dowodu, który przeprowadzimy indukcyjnie ze względu na n. Uwagi poczynione przed sforraulowankra twierdzenia wraz z (I) i (2) dowodzą przypadku n m 1. Zakładając prawdziwość twierdzenia w wymarzę n - I. dowodzimy go w wymiarze a. Dla każdego też należy tylko znaleźć zbiór otwarty U. gdzie a cl/Cż.dU którego twKidzenar jeit prawdziwe. Co więcej, możemy założyć. « *■<«> - /.

Określmy h : A -» R* jako *(x) — (g'(»).....jr"~*(ar). **). Wówczas h\a) •* /.

Sojd na pewnym zbiorze otwartym U", gdzie a € W C A. funkcji h jest 1-1 det *%*)

t0. Możemy więc zdefiniować *• *((/') -* R“ jako *(x) « (z¹.....z*'¹. g*(h '(*))):

wtedy j ■ ł«*. W len sposób wyraziliśmy g jako złożenie dwóch odwzorowań. i których każde zmienia mmc) niż n współrzędnych (rysunek 3.3).

Musimy tajać się kilkoma szczegółami, aby mieć pewność, że * jest funkcję wła-leiwego rodzaju Ponieważ

(/ o*-')'(*(a)) - <**>'(*) • [*'(«)]-* . <*•)'(«).