9491406790

3. PORÓWNANIE ZESTAWIEŃ

Z n-element owego zbioru Z tworzymy k-elementowe podzbiory/ciągi (dla n, k € N* ).

RODZAJE ZESTAWIEŃ	Ilość elementów zbioru Z	Ilość elementów w tworzonych podzbiorach / ciągach		Czy kolejność ułożenia elementów• jest istotna?	Czy elementy mogą się powtarzać?
Kombinacje	n	k	(A < n)	nie	nie
Kombinacje z powtórzeniami	n	k		nie	tak
Wariacje	n	k	(k < n )	tak	nie
Wa riacj e z po wtór zen ia m i	n	k		tak	tak
Permutacje	n	k	(k = n)	tak	nie
Permutacje z powtórzeniami	n	k	(k > n)	tak	tak

Reguła mnożenia - jeżeli pewien wybór zależy od skończonej liczby wielu decyzji, przy czym pierwszo decyzja ma a możliwości, druga - b możliwości, ..., ostatnia - n możliwości, to wybór ten może być zrobiony na a be... n sposobów.

Obliczając prawdopodobieństwo dla zdarzeń będących podzbiorami (bez. powtórzeń) można założyć, że kolejność jest istotna i zastosować regułę mnożenia - ponieważ ilość zdarzeń sprzyjających i elementarnych wzrasta wówczas proporcjonalnie dając te same wyniki prawdopodobieństwa.

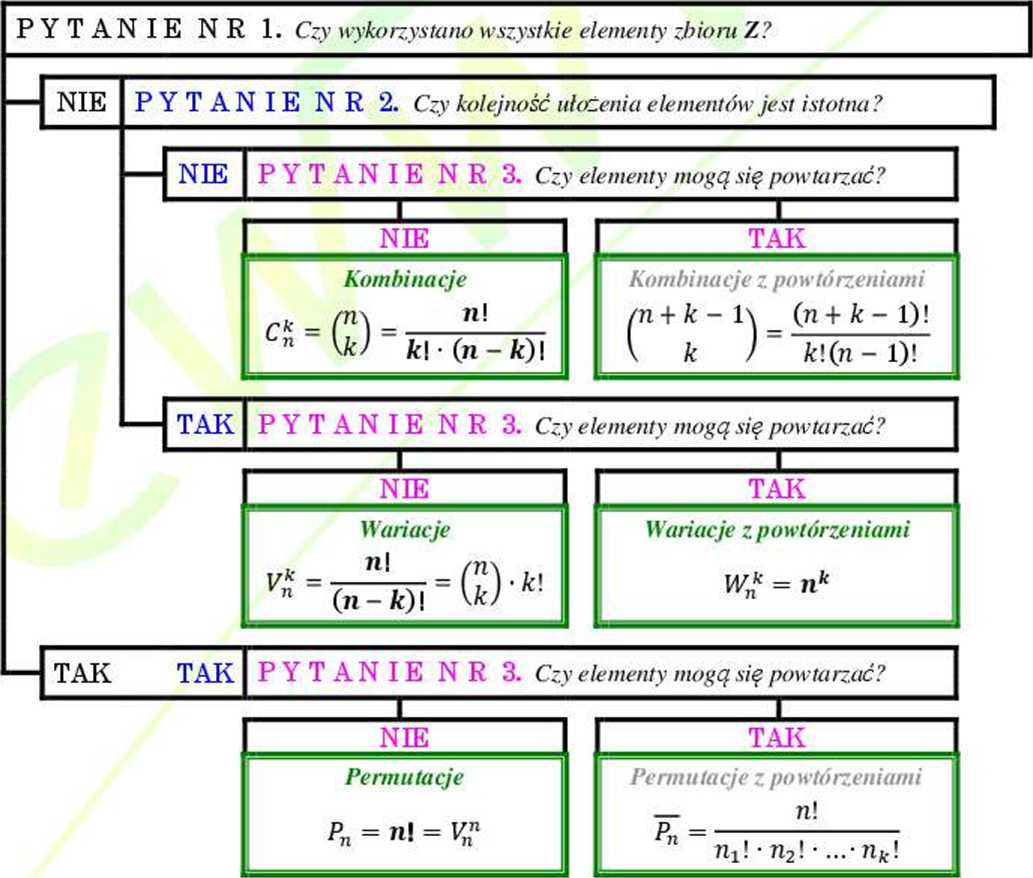
4. UPROSZCZONY ALGORYTM

Podczas tworzenia k-elementowych podzbiorów/ muItizbiorów /ciągów z. n-elementowego zbioru Z, wystarczy umieć odpowiedzieć na trzy poniższe pytania, aby ustalić rodzaj zestawienia.

© Copyright by Ewa Kędzi orczyk

- 323 -

w w w. ma tern a tyka.s osnowiec.pl