1493626998

68 A. Schin«el

et [21J annoncent la formule

1    |< | pour x rationnel,

lim - y (fcr— Efcr)|

^n_~” k^t    **■ i pour x irrationnel

et les travaux [12], [14], [16] en oontiennent une dńmonstration. Cette formule est gńuńralisńe dans [24] et [28] pour x irrationnel de la faęon BUivante:

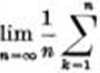
(**-f-y-E(fcx + y))~ J

(y arbitraire).

Iia dernićre ńgalitń montre que la suitę kx est ńquirepartie inod 1, rńsultat prouvń aussi presquc siinultanńment par P. Bohl et U. Weyl. Bientdt (1916) Weyl publia son mńmoire rlassique sur «*e sujet, auque.I se rattache une lonjfue «ćric de travaux de nonibreux auteurs (voir Koksma [VIII], Chapitre VIII).

De la thńorie des approximat.ionR diophanticnnes se rapprochent aussi les travaux [95] (nombroa dits »onnaux) et [684] (fractions continues). DaiiK le premier Sierpiński eonsidf*re les nombres absolument normaux.

Le nombre

X

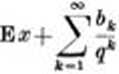
(0 < 6* < q)

est dit norinal par rapport a la base q si

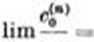
n-+oo ^

»-•*»> ^w

1

9

oń </"’ est le nombre des 5, (1 j < n) qui valent i.

Lorsqu’un nombre donnń est norma! par rapport & toutes les bases possibles (q= 2,3,4,...) il est dit absolument norinal. Cette notion fut introduite par E. Bond, qu» dńmontra que presque tous les nombres rńols sont absolument normaux. En 1909 Borel [IIJ ócrivait: „Dans 1’ńtat actuel do la .Science la dćtermination cffectiYe d’un nombre absolument norinal |*aralt uu problćine des plus dilficilcs”. Sierpiński a dńfini un nombre absolument norinal roninie la borne infńrieure d’un ensemble bien dćterminć de nombres rńels. I/article de H. LcI>chkiio [XI] contient des commentaires inU$ressants sur ee kii jot.

Les travaux sur les algorithmes et les dńvelopj»einent8 [2], [4], [11], [13], [16], [22], [23], [32], [44], [605], [636] ont. un eertain aspect arithmó-tique, mais ils appartiennent en premier licu ii 1’analyse.

Tous les autres travaux de Sierpiński sur la thóorie des nombres appartiennent a la theorie ńlńmentaire et coneernent la drnsibilitl, les congruences, les ćquationa diophantiennes, les fonctions arithmćtiques, les nombres premier*, la thćorie additivc et les pointę de coordonnćcs enti^res.

Le premier groupe contient les travaux [17] (proprtótńs du symbole de Legendre) [5631, [564] (guites pńriodiques modni), [613], [674], [701], [706] (nombres pseudopremiers et lenn gćnćralisations) [696], [702] (suites d’entiers relativement premiera dcux i deux), [562], [613] (eon-gruonces algćbriqucs), [643], [652] (congruenees exponentielles). [513] contient une d^monstration trfcs simple de l’existence d’une infinitć de nombres pseudopremiers (c’est-4-dire d’entier* composćs n qui divisent 2*—2), si n est pscudoprcmier, 2*—1 Test aussi. La m&ne dćmonstration fut donuóe un peu plus tard par Ił. Stcuerwald [XVI11J. L’ćtude des nombres pseudopremiers a 6t6 continuće par d’autres auteurs, tels qiie P. Erdos et A. Rotkiewicz.

Les ćquations diophanticnnes sont 1’objet des travaux [10], [637], [664], [673], [675] (triangles pythagorńens), [628], [665], [671], [678], [685], [698] (óquations quadratiques nonhomogćncs), [622], [626], [662], [679], [682], [687], [689], [711], [719], [720] (syst&nes d’óquations et ćquations de degrń supćrieur), [638], [640] (ćquations esponentielles). Dans rćtude des ćquations diophantiennes Sierpiński n’employait que le* mćthodes ólćmentaires. Particulierement intńressante est la preuve, donnće dans [679] et [687], quc chacune des ćquations

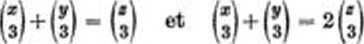
a une infinitń dc Solutions non triviales en entiers positifs x, y, s.

Les travaux sur les fonctions arithnu-tiąues [615], [635], [644], [655], [656], [692], [707], & l’cxeeption de [655], traitcnt des fonctions parti-eulićres telle* que <p, a, etc. non pas de la thćorie gćućralc. Dans [635] on prouve que l’ćqnation <p(x+k) = <p(x) a pour tout k nu inoins uno solution a savoir x= k(p—1), oil p est le plus petit nombre premier qui ne diYise pas k. Plus tard, cette ćquation a ćtń 1’objet des rceherches de P. GiUard, M. Lal, A. Schinzel et A. Wakulic* (voir [IX], [XIV], [XV]). Le travail [615] a un caracttoe plus analytique. On y dćmontre quc pour des suites m*, convenal>lemcnt choisies et pour chaque choix du signe ± on a:

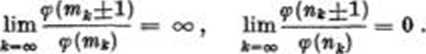
Ce sujet a 6tń abordć ensuite par plusieurs auteurs: P. Erdós, A. Schin-zel, Sbao Pin Tsung et Y. Wang (voir [VJ, [XVI], [XVII]).