3994968259

M.Miszczyński, Materiały do wykładu 7 ze Statystyki, 2006/07

WSPÓŁCZYNNIK KORELACJI RANG

_(Spearmana)_

Współczynnik korelacji rang (Spearmana) ł*s używamy w przypadku gdy:

1.    choć jedna z badanych cech jest cechą jakościowa (niemierzalną), ale istnieje możliwość uporządkowania (ponumerowania) wariantów każdej z cech;

2.    cechy mają charakter ilościowy (mierzalny), ale liczebność zbiorowości jest mała («<30).

Numery jakie nadajemy wariantom cech noszą nazwę rang.

UWAGA ! W procesie nadawania rang stymulanty porządkujemy malejąco, a destymulanty rosnąco.

UWAGA ! W procesie nadawania rang może zdarzyć się więcej niż 1 jednostka o takiej samej wartości cechy (np. A: jednostek). Wówczas należy na chwilę nadać tym jednostkom kolejne rangi. Następnie należy zsumować takie rangi i podzielić przez k (otrzymamy w ten sposób średnią rangę dla tej grupy A: jednostek). W ostateczności każda jednostka z tych A; jednostek otrzyma identyczną rangę (średnią dla danej grupy & jednostek).

Współczynnik korelacji rang (Spearmana) ł*s wyznaczamy wg następującego wzoru:

n

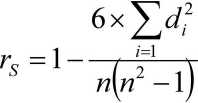
di - różnica pomiędzy rangami dla cechy X i cechy Y