5973829538

typ III: fluktuację przepływu i probabilistyczny charakter transportu ziarna, typ IV: prędkość przepływu strumienia.

Równanie Meyera-Petera i Mullera

Badania radioizotopowe wykazały, że intensywność transportu powinna być obliczana jako suma intensywności transportu poszczególnych frakcji rumowiska dennego w następstwie czego zmodyfikowano równanie Meyera-Petera i Mullera (1948). Modyfikacja (Bartnik 1992, Gładki i in. 1981) dała dużą zgodność obliczeń masy transportowanego rumowiska z pomiarem (Michalik 1990). Wielu badaczy powołuje się na te badania lub stosuje i obliczeniach i modelach matematycznych (Coufal R. 1997, Gręplowska Z. 1997, Lenar-Matyas A., Ratomski J., Witkowska H. 1997, ParzonkaW. 1996, Thome C.R. 1994).

Wspomniana modyfikacja polega na zastąpieniu parametru Shieldsa f = 0,047 przez parametr f dla średnicy frakcji d\, który może być obliczony zgodnie ze wzorem (3). Kolejnym etapem modyfikacyjnym było wprowadzenie zmiennych naprężeń granicznych wg Wanga w funkcji odchylenia standardowego krzywej przesiewu. Została ona również przeprowadzona w oparciu o pomiary radioznacznikowe masy transportowanej rumowiska wleczonego na potoku Targaniczanka, Rabie (Bartnik 1992). Po wprowadzeniu modyfikacji formułę MPM można zapisać:

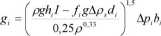
(7)

Wartość zmiennych naprężeń krytycznych może być określona w sposób ogólny z następującego wzoru dla rzek i potoków wyniesie :

dla d, /d_m < 0,6 : e, = 0,0395°-“ / f, = l,786(rf, / dla di /d_m > 0,6 : Ą = 0,0285°“ //, =(d, Id

(8)

(0)

natomiast transport całkowity będzie sumą transportów cząstkowych:

(10)

(11)

9Łi = *łRS

^G.=I gj

Teoria i równanie Bagnolda