614372773

II ° II1

—* 9o II 92 II 9o *9i 9i 9i 92 || 92 || 9i

Tabela 1: Tablica przejść dla automatu z rysunku (2)

1.    Czy na wejściu pojawił się podciąg 01? Jeśli tak, to można zaakceptować dowolny ciąg zer i jedynek, ponieważ ciąg jest zbudowany zgodnie z językiem L. Oznacza to także że następne stany mogą być Sternami akceptującymi.

2.    Jak dotąd podciąg 01 nie pojawił się jeszcze, ale ostatnim widzianym symbolem było 0, jeśli teraz pojawi się 1, oznaczać to będzie, że pojawił się podciąg 01 i następne symbole mogą być dowolnym ciągiem zer i jedynek.

3.    Jak dotąd podciąg 01 nie pojawił się jeszcze, co więcej poprzedni symbol nie został jeszcze podany, bo automat właśnie rozpoczął swoją pracę bądź ostatnim symbolem była jedynka. W takim przypadku automat A nie może zaakceptować słowa, dopóki nie pojawi się zero, a bezpośrednio po zerze jedynka.

Wymienione warunki należy przedstawić za pomocą stanów. Warunek (3) będzie reprezentowany przez stan go- Jest to tym uzasadnione, że jeśli zaczynamy, to musimy wykryć zero, a potem jedynkę. Jeśli będąc w stanie go zobaczymy w pierwszej kolejności jedynkę, to naturalnie nadal musimy pozostać w stanie go- Zapiszemy to w następujący sposób <5(go, 1) = go-

Będąc w stanie go, gdy napotkamy zero to zaczyna obowiązywać warunek (2), czyli <5(go, 0) = g2. Przybliża nas to wykrycia, obecności podciągu 01. Pierwsza sytuacja jak jest istotna w stanie g2 to wykrycie następującego symbolu którym jest zero. Jeśli, tak jest to, <5(g2,0) = g2, co oznacza iż naturalnie pozostajemy w stanie g2-Jednakże jeśli będąc w stanie g2, jeśli wykryjemy zero to wiedząc iż pojawiło się już zero to uzyskaliśmy informację o tym, że wystąpił pod ciąg 01. Przechodzimy do stanu gj, oznaczający stan akceptujący, 8{q%,1) = 9i-

Stan gi może przyjmować, zero bądź jedynkę w dowolnej kolejności ponieważ już wcześniej udało się nam stwierdzić obecność 01. Funkcja przejścia posiada postać 5(gi, 0) = q\ oraz J(gi, 1) = gi-

Zbierając uzyskane informacje, formalnie automat A zdefiniujemy w następujący sposób:

Adaś = ({9o*9i.92}> {0, l},<S,go.{gi})    (4)

Określanie automatu w sposób formalny ze szczegółowym oraz obszernym słownym opisem funkcji przejścia jest żmudne, zabiera sporo czasu oraz co najważniejsze jest mało czytelne choć naturalnie zrozumiałe. Warto jednak stosować dwa inne podejścia w przypadku opisu postaci funkcji przejścia. Diagram przejść dla opisanego automatu prezentuje rysunek (2) natomiast tablica przejść funkcji <5 to tabela (1).

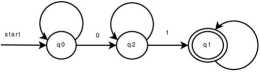
Rysunek 2: Schemat deterministycznego automatu akceptującego wszystkie takie ciągi zbudowane z zer oraz jedynek, które zwierają podciąg 01

1.2 Rozszerzona funkcja przejścia

Rozszerzona funkcja przejścia opisuje sytuację, gdy deterministyczny automat skończony rozpoczyna pracę w dowolnym stanie. Funkcję taką definiuje się wykorzystując standardową funkcję przejścia 8. Rozszerzona funkcja przejścia 8 to funkcja, która otrzymuje stan g i łańcuch w, a jej wynikiem jest stan p, jaki osiągnie