1257951427

92

E’ = E - dla płaskiego stanu naprężenia,

E’ = E/(l — v) - dla płaskiego stanu odkształcenia.

Dla długich czasów (tzn. dużych obszarów objętych pełzaniem) wartość całki C(t) zmierza do C :

C(t -» °<>) = C*    (7.13)

Charakterystyczny czas t_x dzielący przedział czasu na zakresy pełzania krótkotrwałego i długotrwałego obliczymy z zależności:

(7 14)

Dla czasów t « t_x proces propagacji kontrolowany jest przez całkę J lub współczynnik intensywności naprężeń K, natomiast dla t » t_x propagacja kontrolowana jest przez parametr C . Interpolacyjną formułę obejmującą cały przedział czasu możemy zapisać [109, 124]:

C(t) = (1 + Vt)C*    (7.15)

7.1.3. Zakres pełzania pierwotnego

Jeżeli równanie konstytutywne opisujące zachowanie się materiału w pierwszym okresie pełzania, w tzw. pełzaniu pierwotnym, przyjmiemy w postaci [92, 111]:

(7.16)

gdzie:    m, p — parametry,

to pole naprężeń typu HRR wokół wierzchołka pęknięcia, rozwijającego się w obszarze pełzania pierwotnego, opisuje zależność:

\l/(m + 1)

[Bi(l+p)]^{1/(1 + p)}I_mr

^(0, m)

(7.17)

Parametr CJ jest zależny od czasu i definiowany jako:

O

/

CV =

JP(t)

m

Lr

J P(t)^{m(1 + p)} dt

1/(1+p)

C^ł(l + p)	[\ 1 J P(t)^m(1 + p) dt _____i	p/(l + p)
P(t)^mp

(7.18)

gdzie: P(t) jest obciążeniem zależnym od czasu.

Biorąc pod uwagę obszary: sprężysty, pełzania pierwotnego i pełzania ustalonego, możemy napisać następującą formułę wyrażającą wartość parametru kontrolującego rozwój pęknięcia w czasie rozwijania się wszystkich wymienionych stref [111]:

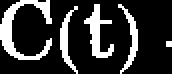
1 + t^/t +

	p/(l + p)
t

\

(p + i)/p

(7.19)

(7.20)

(1 + P)C*

7.1.4. Metody estymacji parametru C

Z przedstawionych powyżej rozważań wynika, że w analizie propagacji pęknięć w warunkach pełzania podstawowe znaczenie ma parametr C . Przez analogię do całki J parametr ten można również interpretować jako różnicę prędkości zmian energii 2 identycznie obciążonych ciał z pęknięciami różniącymi się o nieskończenie małą długość [22]:

(7.21)

(7.22)

P - obciążenie, u - prędkość przemieszczeń.

Opierając się na powyższych zależnościach oraz badaniach doświadczalnych przeprowadzonych na wielu próbkach dla różnej prędkości przemieszczeń można wyznaczyć zależności prędkości propagacji pęknięcia od parametru C* [79, 145].