1935182602

13

0.3. CIĄGI LICZBOWE

a więc ostatecznie dla każdego e > O istnieje no G N że jeśli n> no to I tfń — 1| < e,

co jest równoważne że lim §ćn — 1.

Zachodzi następujące

Twierdzenie 0.3.1 Jeśli ciąg ma granicę, to ma jedyną

Dowod. Niech ciąg będzie zbieżny do dwóch liczb gi,g% G R, załóżmy więc, że \gi — g^l = e. Wtedy istnieje no G N takie, że n > no to \a_n — gĄ < a więc

« = l»i - »I < |o» - 9il + |o» - ®l < | + 2 = e,

co daje sprzeczność. ■

Twierdzenie 0.3.2 (Warunek Cauchy’ego) Ciąg a_n jest zbieżny wtedy i tylko wtedy, gdy

(Ve > 0)(3n₀ G N)(Vn, m > no) \a„ — a_m\ < e. Dowod. Dowód w jedną stronę jest prawie oczywisty, bo mamy

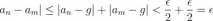
dla pewnej liczby no G N i każdego n > n₀.

Natomiast w drugą stronę, z naszego warunku (kładąc e — 1) dostajemy ograniczoność naszego ciągu. Więc zbiór

A — |.t G R : |{n G N : a_n > x}| = N₀|

jest niepusty i ograniczony z góry, więc ma kres górny g = sup A G R. Udowodnimy, że g = limn-tco a_n. Niech e > 0 będzie dowolną dodatnią liczbą rzeczywistą, to wtedy na mocy kraesu górnego zbioru A, zbiór

.A_£ = |n G N : g + e < a„|

jest skończony, więc istnieje n₀ > max A,, że dla n > n₀ a_n < g + e. Pokażemy teraz, że istnieje no G N n > no to g — e < a_n. Gdyby tak nie było, to

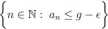
byłby nieskończony, ale g — % < g, to istnieje również nieskończenie mele wyrazów ciągu a_n, że g — | < a_n. Jeśli no G N jest dowolne, to istnieje takie m,n > no że Om < g — e oraz g — | < a_n, to wtedy

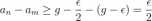
a stąd otrzymujemy sprzeczność z naszym warunkiem Cauchy ’ego ■