2048738909

(33)

a macierze tranzycji określone są wzorem

gdzie

f In (n = ni + n2)	dla	i = 0, j = 0
< TioTj-ij + 7oiTjj_	1 dla	i+j>0 (i,j e Z)
10	dla	i < 0 i/lub j < 0
^ ^c^ ^cII	7oi =	0 0

(34)

Przykład 2. Dany jest dwuwymiarowy układ niecałkowitego rzędu (29), gdzie c*i = 0.7, a₂ — 0.9, a macierze

-0.9    0.7

0    -0.3

1 0

0 1 ’

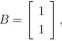
D = [0].

(35)

Poszukiwać będziemy odpowiedzi skokowej układu, tj. wartości wektora odpowiedzi t/(ti, t₂) dla t\,t₂ > 0 na wymuszenie w postaci dwuwymiarowego skoku jednostkowego

0    dla t\ < 0 i/lub t₂ < 0

1    dla t\,t₂ > 0

(36)

przy zerowych warunkach początkowych

Xq(t₂) = 0 dla t₂ > 0, £q(żi) = 0 dla t\ > 0.

(37)

Podstawiając (35), (37), (27) do (31) oraz uwzględniając, że Ni, N₂ = 1 otrzymujemy

x^h(ti,t₂)

x^v(ti,t₂)

= EE^Tt

i=0 j=l

+ E^T‘°

i 2

T[1 + (i + l)ai]r(l + ja₂)

t\

.(<+i)«i

r[l + (*+ l)ai]

- ^T°j

J=o

r[l + (j + l)a₂]

(38)

-EE^t«

t=l j=0

^łl ^l2_

r(i + iafi)r[i + (j +1)02] ’

a macierze tranzycji możemy obliczyć z zależności (33).

Wzór (38) określa odpowiedź skokową układu (29) o macierzach (35). Łatwo pokazać, że współczynniki we wzorze (38) silnie maleją przy rosnących wartościach i oraz j. Zatem, możemy założyć, że liczby i oraz j są ograniczone przez pewne liczby naturalne Li i L₂.

16