img016 2

40 J. Estymacja przedziałowa parametrów

Jub równoważnym mu wzorem

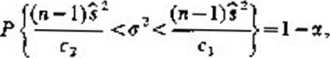
(1.9)

gdzie c, i c₂ są wartościami zmiennej y¹ wyznaczonymi z tablicy rozkładu/² dla n— 1 stopni swobody oraz współczynnika ufności i - ar w taki sposób, by spełnione były relacje

Ponieważ powszechnie używane tablice rozkładu y² podają, prawdopodobieństwo P{x*&X%}* zatem dla określonego współczynnika ufności 1—a wartość Cj znajdujemy z tablic rozkładu y² dla prawdopodobieństwa 1 —natomiast wartość c₂ dla prawdopodobieństwa (rysunek 3). Chcąc wyznaczyć przedział ufności dla odchylenia standardowego <r_T bierzemy arytmetyczny pierwiastek kwadratowy z końców' przedziału ufności dla wariancji o².

‘ Hi?)

c

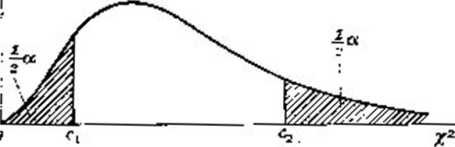
Rys. 3. Rozkład f

Należy zwrócić uwagę, że otrzymany przedział ufności nie jest symetry czny względem wartości s².

Model DL Populacja generalna ma rozkład N(m_t <r) lub zbliżony d normalnego o nieznanych parametrach m i o\ Z populacji tej wy losowań niezależnie dużą liczbę n elementów (n co najmniej kilkadziesiąt). Z prób tej obliczono wartość s- \ Wtedy przybliżony przedział ufności

odchylenia standardowego a populacji generalnej jest określony wzorem

(U 0)

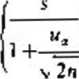
<cr<-

I -a,

edzie u_I jest wartością 2miennej normalnej standaryzowanej U, wyznaczoną w taki sposób dla ustalonego l—ctz tablicy rozkładu AT(0, 1), by spełniona była relacja P { - u_x< U < w_T} = I - ar.

Przykład I. Badając wy trzymałość elementu konstrukcyjnego pewnego urządzenia technicznego dokonano n = 4 niezależnych pomiarów wytrzymałości i otrzymano następujące wyniki (w kG/cm²); 120, 102, 135, 115. Należy zbudować przedział ufności dla wariancji <z² wytrzymałości tego elementu, przyjmując współczynnik ufności l-a=0.96.

Rozwiązanie. Można przyjąć, że rozkład wytrzymałości jest zbliżony do normalnego, zatem zc względu na małą próbę mamy tu do czynienia z modelem t.

Należy najpierw obliczyć z próby wartość ns^z. Mamy

•Ti	z^-' H 1 W
120	4
102	256
135	289
115	9
472	558

Stąd

x=~l² -118,    n$² = 55S.

Z tablicy rozkładu y¹ dla n— J = 3 stopni swobody odczytujemy dla I -^ = 0,98 wartość =0,185 ora? dla 4a=0,02 wartość e₂=9,837. Otrzymujemy zatem następujący przedział ufności dla wariancji o² wytrzymałości:

czyli    56,7 < er <3016.