8 (1088)

34 I. Estymacja przedziałowa parametrów

próbnego uzyskujemy jedynie informację o tym, czy dany element populacji generalnej ma badaną, wyróżnioną cechę jakościową czy też jej nie maj Elementy populacji generalnej możemy więc podzielić wtedy na dwie klasy] elementy wyróżnione w populacji (tj. posiadające badaną kategorię jakcl ściową) oraz niewyróżnione.

Podstawowym parametrem populacji, szacowanym w przypadku badan statystycznych ze względu na cechę niemierzalną (jakościową), jest frakcją (lub po przemnożeniu przez 100 — procent) elementów wyróżnionycłl w populacji, zwana też wskaźnikiem struktury w populacji, gdyż często jest to tylko jeden element całej tablicy statystycznej ujmującej strukturę popUa lacji generalnej ze względu na badaną cechę.

Wskaźnik struktury populacji, którego wartość jest ułamkiem właściwym: (lub procentem mniejszym od 100), oznaczamy zwykle symbolem p (nie; należy mylić tego symbolu z prawdopodobieństwem jakiegoś zdarzenia; ■ losowego).

Przedział ufności dla wskaźnika struktury p, czyli dla frakcji elementów] wyróżnionych w populacji, otrzymujemy jak zwykle z odpowiedniego] rozkładu estymatora tego parametru. Najlepszym estymatorem, uzyskał nym metodą największej wiarygodności parametru p, jest wskaźnik strukturV z próby m/n, gdzie m oznacza liczbę elementów wyróżnionych znalezionych^ w losowej próbie o liczebności n.

W zależności od wielkości próby n można budowę przedziału ufności dla p oprzeć albo na dokładnym rozkładzie estymatora mjn, albo też na jego rozkładzie granicznym (w dużej próbie). Wyznaczanie przedziału] ufności dla wskaźnika struktury p z małej próby nie'jest sprawą prostą (istnieją gotowe tablice podające przedział ufności w tym przypadku-zamieszczone np. w Tablicach Statystycznych pod red. W. Sadowskiego)! toteż pominiemy to zagadnienie.

Najczęściej szacujemy frakcję p elementów wyróżnionych (lub procent} w populacji, w oparciu o wyniki dużej próby (n — co najmniej 100). Wtedjl korzystając z faktu, iż estymatory uzyskane metodą największej wiarygodno^ ści mają rozkład asymptotycznie normalny, możemy wyznaczyć przybili żony przedział ufności dla parametru p.

Model. Populacja generalna ma rozkład dwupunktowy z parametrem pi tzn. elementy populacji są podzielone na dwie klasy, przy czym frakcją] elementów wyróżnionych w populacji wynosi p, które nie jest małym ułamH

kiem (p>0,05). Z populacji tej wylosowano niezależnie dużą liczbę n elementów do próby (n> 100). Wtedy przedział ufności dla wskaźnika struktury p populacji generalnej jest określony przybliżonym wzorem:

(1-6)

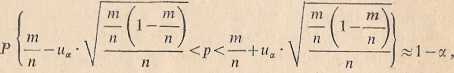
gdzie m jest liczbą elementów wyróżnionych znalezionych w próbie, a u_K jest odczytaną z tablicy rozkładu normalnego N(0,1) wartością zmiennej normalnej standaryzowanej U, w taki sposób, by spełniona była relacja P{-|w_a<Ł/<«J=l --a dla ustalonego z góry współczynnika ufnóści 1 —a.

Przykład. Chcemy oszacować, jaki procent pracujących mieszkańców Warszawy jada obiady w stołówkach pracowniczych. Pobrano w tym celu n = 900 osób wylosowanych niezależnie do próby i znaleziono w tej próbie m=300 osób, które jedzą obiady w stołówkach. Przyjmując współczynnik ufności 1—a=0,95 zbudować przedział ufności dla procentu badanej kategorii pracujących w Warszawie.

Rozwiązanie. Z treści zadania wynika, że próba była duża, toteż przedział ufności dla szacowanej frakcji p pracowników można wyznaczyć według wzoru (1.6). Dokonujemy niezbędnych obliczeń:

=0,333,

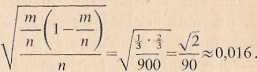
m 360 _ 1 ~i 900 3

Z tablicy rozkładu normalnego N(0, 1) dla 1 — a = 0,95, tzn. dla a=0,05, znajdujemy wartość u_K= 1,96. Otrzymujemy zatem następujący przybliżony przedział ufności:

0,333 -1,96 • 0,016 <p <0,333 + 1,96-0,016,    czyli 0,302 <p <0,364.

Zatem przedział liczbowy o końcach 30,2% i 36,4% z ufnością 0,95 obejmuje nieznany procent pracujących mieszkańców Warszawy, jedzących obiady w stołówkach pracowniczych;