img020 3

4$ 1. Estymacja przedziałowa parametrów

gdzie /> jesi spodziewanym rzędem wielkości szacowanego wskaźnika struk-„ tury (w\ rażonym jako ułamek wjaściwy), q = ] -p, J jest dopuszczalnym maksymalnym błędem szacunku frakcji p (wyrażonym też w ułamku właściwym), to jest wartością odczytaną w zwykły sposób (tak jak w modelu 1) z tabhc> rozkładu A'(U. 1) dla współczynnika ufności i— 2;

b) jeżeli nie znamy rzędu wielkości szacowanego wskaźnika struktury p_y to przyjmując za iloczyn pq jego największą wartość j, otrzymujemy następujący wzór na liczebność próby:

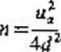
Jeżeli prawdziwa wartość p spełnia nierówność p~£\, to obliczona powyższym wzorem wielkość próby jest za duża (ten. stosując tak wielką próbę otrzymujemy maksymalny błąd szacunku mniejszy niż założona wartość cf)>

Przykład 1. Zbadać, ile niezależnych obserwacji powinna liczyć próba, by na jej podstawie można było oszacować średni czas wykonywania przez robotnika pewnej operacji technicznej z błędem maksymalnym 20 sek, przy czym przyjmujemy współczynnik ufności 0,95. Wiadomo, że czas wykonywania tej operacji technicznej jest zmienDą losową o rozkładzie normalnym .Y(m,40).

Rozwiązanie. 2 treści zadania wynika, że znana jest wariancja populacji o-² = 1600. więc mamy do czynienia z modelem J. 2 tablicy rozkładu A'(0i 1) dla I-r = 0.95_t tzn. dla et = 0,05, odczytujemy wartość u* = 1,96. Stosując odpowiedni dla modelu I wzór (UJ), otrzymujemy

3,$4-4= 15,36 *16

• >600

^ ~ 202

obserwacji.

Przykład 2. Należy oszacować średnią wartość masy pewnej substancji wydzielającej się w pewnym doświadczeniu chemicznym. Ile niezależnych doświadczeń należy przeprowadzić, aby przy współczynniku ufności 0,95 oszacować metodą przedziałową tę średnią masę z błędem maksymalnym 0,01 g, jeżeli próba wstępna 5 niezależnych doświadczeń dała następujące wyniki (w g): 2,10, 2,12, 2,12, 2,16, 2,10?

§ 1.4. Wyznaczanie niezbędnej Liczby pomiarów dla próby

49

Rozwiązanie. Z treści zadania wynika, że mamy do czynienia z modelem JI, przy czym z próby wstępnej należy wyznaczyć wartość s². Mamy

Sląd

x =

=2,12,

- »_0,00 ^{S —}    4

0,0006.

x(	Ui - i)^2
2,10	0.0004
2,12	0
w*	0
i 2.16	D.0016
2,10	0.0004
10,60	0,0024

J0.6

~S~

Z tablicy rozkładu t Studenta dla 4 stopni swobody i dla 2 = 0,05 odczytujemy wartość =2,776. Stosując odpowiedni dla modelu Ii w»zór (1.12) na liczebność próby, otrzymujemy

n

(2.7TS)¹ • O.0<JO«> (O.&l)*

=7,73-6=46,38*47.

Ponieważ zi=47>5=/r₀, wice oprócz pięciu posiadanych wyników pomiarów należy jeszcze dokonać 42 pomiarów masy wydzielającej się w tej reakcji substancji.

Przvklad 3. Zbadać, tle należy wylosować niezależnie studentów pewnej uczelni, do próby, by oszacować procent studentów tej uczelni palących papierosy, z błędem maksymalnym 5%, przy współczynniku ufności 0,90. Przypuszcza się, że szacowany procent palących studentów' jest rzędu 70 %.

Rozwiązanie. Z treści zadania wynika, że mamy dc czynienia z modelem III a. Z tablicy rozkładu normalnego JV(0, 1) dla 1 — a=0,90 odczytujemy wartość i/*=l,64. Mamy tf=0,05 oraz p = 0,7, C2yli 0,3. Stosując wrzór (1.13) otrzymujemy niezbędną wielkość próby rr.

U.T-0,3    564<»

lO.OS>»

= - j-r- — 225,96 « 226

studentów.

Ą Grefi