img019 3

46 I. Estymacja przedziałowa parametrów

szacunek Tego parametru. Stąd dążenie do zapewnienia sobie z góry dobrej dokładności szacunku. Można to uczynić przez dobranie dostatecznie dużej próby.

Na wielkość maksymalnego błędu szacunku, tj. połowę długości przedziału ufności, istotnie wpływa obok współczynnika ufności ustalona wielkość próby n. JcżcJi nie będziemy traktować liczebności próby n jako ustalonej i przekształcimy odpowiednie wzory na połowę długości przedziału ufności, to okaże się, że na odwrót — liczebność próby potrzebna do dokonania szacunkuparametru z ustaloną dokładnością uwarunkowana jest między innymi żądanym stopniem dokładności szacunku.

Należy- wyraźnie podkreślić,' że nie zawsze można odpowiedzieć na najczęściej formułowane pod adresem statystyki matematycznej pytanie praktyków' - jak wielka powinna być próba, by szacunek parametru był dokonany Z zagwarantowaniem żądanej dokładności. Po pierwsze dlatego, że nic zawsze da się otrzymać ze wzorów na przedziały ufności wzorów na liczebność próby (np, nie można tego zrobić w przypadku szacowania wariancji <7² populacji), a po drugie dlatego, że nie zawsze mamy potrzebne do tego informacje o populacji (np. potrzebna jest informacja o wariancji populacji).

Dla dw'óch najczęściej szacowanych parametrów populacji, a mianowicie dla wartości średniej m ora2 wskaźnika struktury p, można otrzymać wzory na minimalną liczebność próby potrzebną do oszacowania tych parametrów 2 żądaną z góry dokładnością. W zależności od informacji, jakie mamy przed dokonywaniem szacunku średniej lub wskaźnika struktury, można niezbędną liczebność próby w losowaniu niezależnym ustalić według wzorów podanych w poniższych modelach.

Model I. Populacja generalna ma rozkład normalny N(m, n) bądź zbliżony do normalnego. Wariancja populacji o² jest znana. Chcemy oszacować nieznaną średnią wartość m populacji na podstawie próby złożonej z n niezależnych pomiarów. Jeżeli żądamy, by przy ustalonym współczynniku ufności 1-a maksymalny błąd szacunku średniej m (tj. połowa długości przedziału ufności) nie przekroczył z góry danej liczby d. to niezbędną do uzyskania tego celu liczebność próby n oblicza się ze wzoru

u-o-

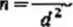
§ LA. Wyznaczacie niezbędnej liczby pomiarów dJa próby

gdzie u₇ jest wartością zmiennej normalnej >'(0. 1) odczytany z tablicy dla 1 —« w taki sposób, że P{~u_a< U<u_a) -1 —a, a <i — dopuszczalnym, ustalonym z góry maksymalnym błędem szacunku średniej ni.

Jeżeli obliczona liczebność próby n jest ze względów praktycznych za duża, to mniejszą liczebność próby wyznaczymy z tego wzoru, zwiększając odpowiednio dopuszczalny błąd szacunku ci.

Model TT, Populacja generalna ma rozkład JV(/w, o). Wariancja o¹ po-pulacji jest nieznana, ale znana jest wartość statystyki s\ uzyskana z małej próby (wstępnej) o liczebności n_Q elementów. Chcemy oszacować średnią m populacji metoda przedziałową ze współczynnikiem ufności 1 —a w taki sposób, by maksymalny błąd szacunku nie przekroczył z góry danej liczby d. Niezbędną do tego celu liczebność właściwej próby n usta la się według wzoru

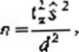
[i. 12)

gdzie

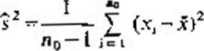
jest wariancją z małej próby wstępnej o liczebności n_0y f_x jest wartością zmiennej t Studenta odczytaną z. tablicy’ tego rozkładu dla współczynniku ufności 1 —a i dla n₀-1 stopni swobody w laki sposób, że P{- t,<i<t₉} =

Jeżeli obliczona (z dokładnością do 1, przy czym zaokrąglamy zawsze w górę) liczebność właściwej próby _n spełnia nierówność «=$/?<>, to liczebność ruy próby wstępnej jest wystarczająca- Jeżeli zaś ir>n_Q, to należy dolosować do właściwej próby jeszcze «-n₀ elementów.

Model DL Populacja generalna ma rozkład dwupuaktowy z parametrem p ttzn. p jest frakcją jedynek lub elementów wyróżnionych w populacji). Należy oszacować metodą przedziałową parametr p tak, by przy współczynniku ufności 1— a. maksymalny błąd szacunku wskaźnika struktury p nie przekroczy! danej z góry liczby d. Przy tym

a) Jeżeli znamy spodziewany rząd wielkości szacowane; frakcji p₇to niezbędną wielkość próby ustalamy według wzoru

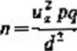
(M3)