2 (2004)

22 I. Estymacja przedziałowa parametrów

gdziĆ x oznacza obliczoną z wyników x_t próby średnią arytmetyczną według wzoru

22 I. Estymacja przedziałowa parametrów

X =§

£ x_t,

n i=i

1 — a jest prawdopodobieństwem przyjętym z góry i nazywanym współczynnikiem ufności, a u_a jest wartością zmiennej losowej U mającej rozkład normalny standaryzowany. Wartość u_a dla danego współczynnika ufności 1—a wyznacza się z tablicy dystrybuanty rozkładu normalnego N(Q, 1) w taki sposób, by spełniona była relacja P{—u_a<U<u_a}=l—a (rys. 1). Na przykład dla najczęściej przyjmowanego współczynnika ufności 1—a= =0,95 mamy w* =1,96.

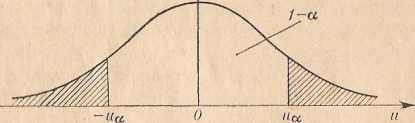
Rys. ł. Rozkład normalny standaryzowany

Model U. Populacja > generalna - ma rozkład N(m, o). Nieznana jest zarówno wartość średnią w, jak i odchylenie standardowe o w populacjij Z populacji tej wylosowano niezależnie małą próbę o liczebności n ele-; mentów. Przedział ufności dla średniej m populacji otrzymuje się wówczas: według wzoru

(1.2)    p\x—t_a' ■ ^S    <m<x + t_a • -7=> = 1—a

I    V« —1    yjn — lj

lub według wzoru równoważnego

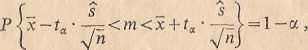
(1.3)

gdzie x oznacza średnią arytmetyczną obliczoną z wyników próby, s i s są odchyleniami standardowymi z próby obliczonymi według wzorów

^(,,4) s*■>/« £

Wartość t_a oznacza wartość zmiennej t Studenta odczytaną z tablicy tego rozkładu dla «-l stopni swobody w taki sposób, by dla danego , z góry prawdopodobieństwa 1 — a spełniona była relacja P{—t_a<t<t_a}— 1 — a (rys..; 2).

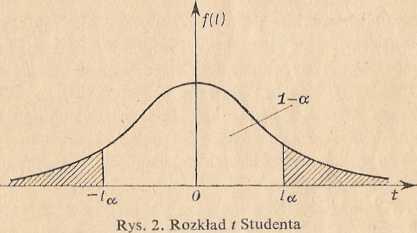
Model m. Populacja generalna ma rozkład N(m, d) bądź dowolny inny rozkład o średniej m i skończonej wariancji cr² (nieznanej). Z populacji tej pobrano do próby n niezależnych obserwacji, przy czym liczebność próby jest duża (co najmniej kilka dziesiątków). Wtedy przedział ufności dla średniej m populacji wyznaczamy ze wzoru jak w modelu I, z tą tylko różnicą, że zamiast o we wzorze tym używamy wartości odchyleń standardowych s lub s obliczonych z próby. Ze względu na dużą próbę, wyniki jej grupuje się zwykle w szereg rozdzielczy o r klasach i wtedy wygodnie jest obliczać x oraz s według wzorów

d-5)

*=— ⁿ jf¹

- Z Wmm

¹ n j=i

o

gdzie Xj oznacza środek poszczególnego przedziału klasowego, a ig jego liczebność. Gdy liczba r przedziałów klasowych jest mała, tzn. gdy długość^