2852046718

3. Co każdy logik umieć powinien ... 19

3. Co każdy logik umieć powinien ...

3.1.    Zadania

3.1.1.    Stare sylogizmy

1. Znajdź wniosek (w oparciu o diagramy Venna) na podstawie następujących przesłanek:

Ludzie młodzi lubią spacerować.

Studenci są młodzi.

Rozwiązanie:

1. Zastępujemy nazwy w przesłankach za pomocą odpowiednich zmiennych oraz uzupełniamy zwroty kwantyfikujące. W języku polskim obowiązują pewne „niepisane” zasady: zdanie z nazwą w liczbie mnogiej traktujemy jako ogólne (a więc dodajemy zwrot „każdy” na początku), dla zdań szczegółowych kwantyfikacja jest wskazywana przez zwroty „pewne”, „niektóre”, czasem przez zastąpienie czasownika „jest (są)” przez „bywają”, itp. Otrzymujemy: „młody człowiek” = M, „student” = S, „ten, który lubi spacerować” = P

MaP

SaM

?

2. Rysujemy diagram Yenna:

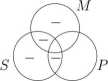
3. Analizujemy diagram pod kątem relacji między S a P. Widzimy, że na diagramie wszystkie S nie będące P są „wykreślone” (na odpowiednich obszarach diagramu są czyli nie istnieją S nie będące P, a stąd wynika, że zadanie SaP jest prawdziwe. A zatem szukanym wnioskiem jest zdanie: „Każdy student lubi spacerować”.

a)    Polacy są pracowici.

Żaden miś koala nie jest pracowity.

b)    Pewni Żydzi są bogaci.

Wszyscy Eskimosi nie są Żydami.

c)    Żadne tłuste stworzenie nie biega dobrze.

Pewne charty biegają dobrze.

d)    Śliwki w czekoladzie są słodkie.

Niektóre słodkie rzeczy są łubiane przez dzieci.

e)    Wszyscy bladzi ludzie są flegmatyczni.

Nikt nie wygląda poetycznie, o ile nie jest blady.