348068283

R. Kadaj: WYKŁADY Z GEODEZJI na kierunku BUDOWNiC 7WO. Temat 9: Podstawy teorii Mędów i wyrównania obserwacji

Elementy teorii błędów maksymalnych na przykładzie błędów zaokrągleń

Błąd e liczby (miary) przybliżonej (zaokrąglonej) x względem miary dokładnej x* :

e = x-x*

Błąd bezwzględny: | e \;

Błąd względny:    rj = \ e \ /\x\

Maksymalny (graniczny) błąd bezwzględny liczby przybliżonej:

możliwie najmniejsza (według posiadanych informacji) liczba A spełniająca warunek:

| e | < A

Błąd zaokrąglenia liczby dziesiętnej na pozycji t:    \e \ < 'A JO¹ = A

C3

c2

Ci

^c0

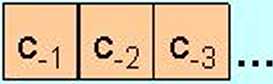
A = ^!A J0~^s (t = - 3 = pozycja zaokrąglenia)

Zapis liczby Z w systemie pozycyjnym o podstawie p (np.: p = 10, p = 2):

X = Zc_t ■pⁱ (i - pozycja cyfry c_t)

np.:    (128.53)₁₀ =1 ■ JO² + 2 ■ 10^l +8 -10°+ 5 ■ 10~^l+3 ■ 10~²    \e\ < ^lA 10~²

(1011.01)₂ = 1 -2³ + 0-2² + 1 -2^l +0 ■ 2~^l+l-2~²    \e\<Zi2~²

Maksymalny (graniczny) błąd względny liczby (miary) przybliżonej:

możliwie najmniejsza (według posiadanych informacji) liczba S spełniająca warunek:

T] <S

188