348068287

R. Kadaj: WYKŁADY Z GEODEZJI na kierunku BUDOWNiC 7WO. Temat 9: Podstawy teorii Mędów i wyrównania obserwacji

Proste przykłady oceny błędu maksymalnego - c.d. Reguły zaokrągleń Krylowa - Bradisa

R. Kadaj: WYKŁADY Z GEODEZJI na kierunku BUDOWNiC 7WO. Temat 9: Podstawy teorii Mędów i wyrównania obserwacji

Mnożenie / dzielenie liczb przybliżonych - maksymalny błąd względny i jego zależność od ilości cyfr dokładnych

y = A^xi, x₂) = x_I -x₂; A_y = \x₂\ ■ Aj + \x_ź\ ■ A₂ /: \y | =| x_ź\ ■ \x₂\

■^y^//ly\⁼^i^//\^xj\ ⁺ ^2 / 1*2.1 ^=> 8y ⁼ Ą ⁺ $2 y = x_I/x₂ A_y = (1/ \x₂\) ■Aj + \-x₂/x₂²\ -4    /: |y| = \xj\/\x₂\

■Ay/\y\ ⁼ <^1 /\^xi\ ⁺ a₂/\^x2\ ⁼> Sy = s₂ + s₂

Zależność maksymalnego błędu względnego od ilości (n) cyfr dokładnych:

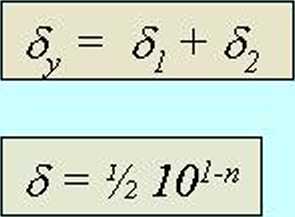
Przykładowo:    n = 1 => S = 0.5, n=2 => S = 0.05, n = 3 => S = 0.005, n=5 => S = 0.00005

maksymalne błędy bezwzględny względny

Aj = 14 10'¹    Sj = 14 10'¹

4; = 14 ł O'³    S₂ = !4 10'⁴

Przy mnożeniu / dzieleniu liczb przybliżonych (zaokrąglonych) w wyniku zachowujemy tyle cyfr znaczących ile je ma argument o najmniejszej ilości cyfr znaczących.

191

1

możliwe cyfry dokładne    cyfry niepewne