3576900827

* PLN 3M Depo: 4.00%, PLN FRA3x6: 5.00%, USD FRA3x6: 2.00%.

(a)    Oblicz stopę 3M depozytu dolarowego przy założeniu, że w okresie 3M na rynku nie ma możliwości do arbitrażu.

(b)    Czy przy powyższych danych istnieją na rynku w okresie do 6M możliwości do arbitrażu ? Jeśli tak, opisz strategię arbitrażową i oblicz dzisiejszą wartość wolnego od ryzyka zysku.

Zadanie 3. (15 punktów)

Wypłata opcji azjatyckiej cali w chwili t <T (T jest czasem wygaśnięcia opcji) wynosi

max(A(f) — K, 0),

gdzie K jest ceną wykonania a

'⁴w = ^E^s(^f<)

jest dyskretną średnią arytmetyczną naliczoną do chwili t na podstawie wartości cen akcji w chwilach ti <    < ... < t_n < t. Jeśli t < ti, to A(t) = 0. Ostatnia chwila czasu

z której wartość ceny akcji jest uwzględniana do obliczenia średniej pokrywa się z czasem wygaśnięcia opcji T.

Rozpatrzmy 9-cio miesięczną amerykańską opcję azjatycką cali na akcję (niepłacącą dywidendy). Cena wykonania tej opcji wynosi K — 105 PLN. Dyskretna średnia arytmetyczna jest obliczana w chwilach ti = (3i)M, gdzie i = 0,1,2,3.

Wyceń tę opcję na trzy-okresowym drzewie dwumianowym przy następujących danych:

*    bieżąca cena akcji wynosi 100 PLN,

*    zmienność akcji wynosi 27.953%,

*    3M stopa procentowa wynosi 11.6%, stopa FRA3x6: 9.41%, stopa FRA6x9: 8.32%. Zadanie 4. (5 punktów)

Rozpatrzmy opcje europejskie o czasie trwania T, które są w chwili bieżącej at-the-money forward, to znaczy takie których cena wykonania K i bieżąca cena akcji S spełniają warunek

S = K exp(—(r — S)T),

gdzie r jest stopą wolną od ryzyka, a 5 stopą (ciągłej) dywidendy.

Pokaż, że w tym przypadku ceny opcji cali i put są takie same i wynoszą

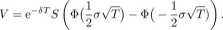
Ponadto, pokaż, że dla małych wartości a\/T, zachodzi przybliżony wzór V aOAe-^STScVf.

W powyższych wzorach a oznacza zmienność akcji, a $ dystrybuantę rozkładu AT(0,1).