5439978896

224

PRZEGLĄD ELEKTROTECHNICZNY

5 500² . 0,8 12 000 000

2,02 omów (na jedną fazę)

7 ^v~

Z =    .cos %

N

W myśl założenia zmniejszenia impedancji przy zwar ciu do połowy wartości będzie:

Zł = - . Z = 1,01 W

2

R_h = 1,01 . 0,8 = 0,808 Si

uwzględniania, widzimy, że przez uwzględnienie obciążenia impedancja zewnętrzna, na którą przy zwarciu generator pracuje, zmalała z 0.993 omów na 0,5 oma; skutkiem tego prąd zwarcia w generatorze wzrósł z 2 980 A na 3 520 A. napięcie na zaciskach zmalało z 5 130 V do 3 050 V, a więc i prąd zwarcia w miejscu zwarcia spadł w tymże stosunku z 2 980 A do 1 772 A.

4" Ru * 2*

Cfy + /?_A)² + (u> L_b + ^ L_a)² 0.808 . 0,993² 4 0,767 . 1.01³ (0,808 -I- 0,767y + (0.61 + 0,629)-

X =

= 0,31 Si

u>L_b- I 1,01* -0.808* = 0,61 V.

Pozatem:

Z_k=\ R-_k + i»L\ = V 0,767² -f 0.629- = 0.993 S2 a więc:

R =

0.394 Si

⁴⁰ Lb • ^z\ + ⁴⁰ Lk • ^Z'b

',R_b + R_ky + (“>!* I- o>L_k)^:

0,61.0.993² + 0,628.1,01*

(0.808 + 0.767)³ -j- (0.61 + 0,629)*

B. Wyznaczenie uderzeniowego prądu zwarcia.

Ścisłe wyliczenie wielkości i przebiegu uderzeniowego prądu zwarcia napotyka na wielkie trudności, gdyż mamy tu, jak wiadomo, do czynienia ze stanem nieustalonym.

Prąd początkowy zwarcia zawiera w sobie oprócz składowej prądu ustalonego zwarcia dwie składowe zanikające: prądu wyrównawczego zmiennego i stałego. Do powyższych dodaje się jeszcze geometrycznie prąd obciążenia, jaki płynął przez generator przed zwarciem.

Praktycznie interesuje nas znajomość maksymalnej amplitudy prądu uderzeniowego, oraz przebieg zaniku jego składowych wyrównawczych. Ograniczymy się do przypomnienia znanych wzorów empirycznych.

Przy zwarciu na zaciskach generatora stosunek maksymalnej amplitudy prądu uderzeniowego do normalnego prądu wynosi:

Zastosujemy w obliczeniu metodę obrachunkową:

X \ X. 0.31+0.44

0,44

/Jlr~\

= 1.7 U

✓ 3

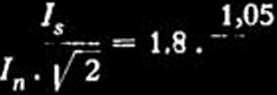
(18)

\    5 250

0.328 •---- =2.76 Si

/ 2 260 . y 3

I 1

«

\ 0,418

(a . X₈y + a . X_q . X_s + R\

X_q.X_s-\-a.X\

0.75- + 0,75.2,76 + 0.394²

Zakładamy tu wzbudzenie w chwili zwarcia, odpowiadające napięciu o 5% wyższemu od nominalnego napięcia generatora. powinno dla turbogeneratorów (z gładkim wirnikiem) odpowiadać stosunkowemu napięciu rozproszenia samego stojana; w braku odpowiednich danych musimy się zadowolić użyciem wartości całkowitego rozproszenia generatora.

Przy zwarciu w sieci jllj będzie:

2.76.0.44 + 1.7.0,44*

= 1.81

gdzie:

dl

1,05

_r V - ^{1 8} / ^,-----

Ai •}/ 2    j/i(a . e_sy -1- e_r ² (a — o_r)²

^mLk

(19)

604

144

4.2 i a = 1.81

r, + R_k

otrzymamy przez ekstrapolację:

(3.5 - 3)

(3,49 —3.02). (4.2 —3.5)

(2

— j 3.50 + i ostatecznie:

(3.5 — 3)

(3.50 —3,09). (4,2 —3.5) (3.5 - 3)

1.05.5 000

.4.13 = 3 520 A.

_l_3

U

r_s — opór omowy jednej fazy uzwojenia stojana.

R_k — opór omowy zewnętrznego obwodu zwarcia (na jedną fazę).

Dla bardzo małych wartości r₈ (dla generatorów dużej mocy) będzie:

c_r^a (a — a_r)² = (s_r . a — e_r . o_r)² =

} 3.(2.76+ 1,81.0.44)

Napięcie na zaciskach generatora będzie:

U 3 520 . |/0,394> + 0,31^J. \ 3 = 3 050 V.

Prąd w miejscu zwarcia:

_r 3 050

«/-—    ■1 772 A.

0.993. ]/ 3

Prąd w odbiornikach:

^°⁵⁰/    ³ 1 742 A

1.01 . |/ 3

Z porównania obu wypadków zwarcia w końcu kabla zasilającego:    przy uwzględnieniu obciążenia i bez jego

tak iż:

^Jn • |/ 2

•^r.*l3

U

= 1.8.-

(r, + R_k) 3 . 7„² . R„

1,05

+

3 - L. R U

120)

Wielkości prądu zwarcia uderzeniowego są jednakowe

przy zwarciu trzy- i dwufazowem.

Rys. 7 przedstawia zmianę w czasie amplitudy składowej zmiennej prądu uderzeniowego dla przeciętnych turbogeneratorów i zwarcia na zaciskach (wg. REH/1929).