5521243837

1014

PRZEGLĄD TECHNICZNY

1927

le przekroju krzyżulca (wydłużenie pa«sów pomijamy). Z drugiej strony, tg <p = ^ ,?gdyż y" o-

znacza rzędne możliwego wygięcia się osi pręta wskutek działania sił poprzecznych.

Wobec tego ustawia Engesser równanie następujące:

d/'____9.___ (₆)

dx Et cos^.sinco

Ze wzoru (6) oraz z następującego wzoru (1)

Q = ^(Fy),.....(7)

wyrażającego zależność między siłą poprzeczną a momentem zginającym w ten sam sposób, jak dla pręta pełnego, wyznacza Engesser spółczyn-nik a. Zadanie jest więc rozwiązane, gdyż wzór (4) daje wartość podłużnej siły krytycznej w pręcie, a wzór (7) odpowiednią siłę poprzeczną, na którą należy obliczać kratę pręta.

Z podobnej metody korzysta Engesser również i do obliczenia pręta ramowego.

Metody drugiej grupy oparte są bezpośrednio na pracach laboratoryjnych i dotyczą prętów złożonych poza granicami sprężystości. Należą tu prace Krohn‘a, Gerard‘a ^i:i), Schal.ler‘a, Saliger‘a i innych. Typową jest tu praca Krohn‘a. Jest ona oparta na własnych, omówionych wyżej, doświadczeniach Krohn‘a oraz na dawniejszych doświadczeniach Tetmajera, nie jest jednak pozbawiona pewnej sztuczności.

Stąd na podstawie równań (8) i (9) Krohn dochodzi do wzorów następujących:

• _*/ h__ _{

°”T"136 ti — r • • £ ■ ¹¹³¹

ip _p ._____ 1(14)

Siła P, odgrywa tu rolę siły krytycznej, z którą ma być porównana rzeczywista siła, działająca w jednym pasie pręta.

Siłę poprzeczną w pręcie, w chwili wygięcia

, , _n dM

się jego, otrzymuje Krohn ze wzoru: —

Przyjmując dla odkształconej pręta przebieg cosi-

nusowy =Sjcos’/y (początek osi spółrzędnych

w środku pręta) i wstawiając tu o ze wzoru (13),

otrzymuje on, iż Q = ^g, gdzie F oznacza pole

przekroju poprzecznego pręta. Na siłę tę należy obliczać kratę pręta.

Wreszcie, metody trzeciej grupy dotyczą prętów, podległych jednoczesnemu ściskaniu i zginaniu, przyczem poszczególne części prętów mogą •tu być dokładnie obliczone, gdyż, jak było powiedziane, mtmośród siły podłużnej jest wiadomy. Należą tu prace Miiller-Breslaua ¹⁴), Kayser'a ¹⁵) i moja.

iMiiller-Breslau rozważa pręty ramowe i kratowe pod działaniem siły podłużnej, równoległej do osi pręta, o mimo środzie a. Wprowadza on do

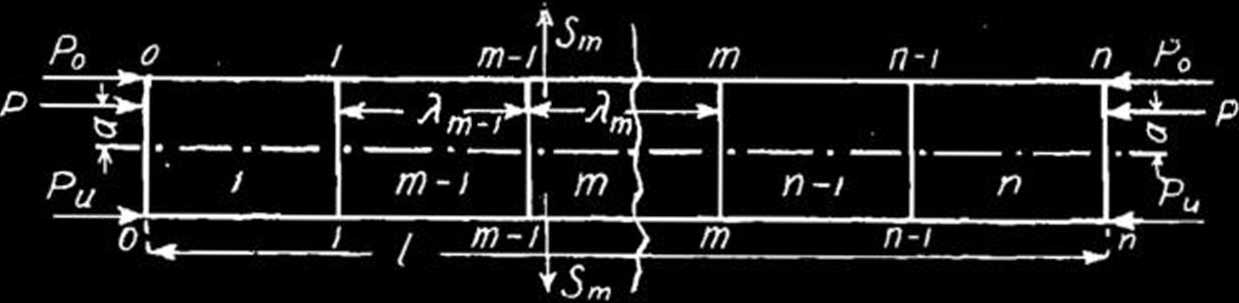
Rys. 6.

Krohn uważa, że siła, ściskająca pręt złożony w chwili wygięcia, nie jest rozłożona równomiernie między pasy pręta, gdyż wygięcie się pręta wywołuje różnice w obciążeniach pasów na niekorzyść pasa, znajdującego się od strony wklęsłej. Siła działająca w tym ostatnim pasie wyraża się więc wzorem:

~ ^P ( 2 h )' ' ' ' ' ®

w którym h jest to odległość między pasami* Ze wzoru na ściskanie mimośrodkowe dla chwili wyginania się pręta, ustawia Krohn zależność następującą:

Porównanie wzoru (9) ze wzorem Tetmajera dla naprężenia krytycznego, t. j. ze wzorem:

K₀ =-J-= 3,1 -0,0114-1- ^kg, . . (10) F i cm¹ 7

doprowadza Krohn'a do twierdzenia, że ostatnie wyrazy w obydwóch wzorach oznaczają tę samą wielkość, czyli że:

Po l

^ = 0,0114 —.....(11),

/ W

skąd 5 = 00,114.... (12)

^,3) Gustave L. Gerard, Rćsistance des pieces compri-m6es & treillis, Revue universelle des Mines, 1913, 1914,.

swego obliczenia wielkości następujące, odpowiadające każdemu przedziałowi pręta (rys. 6).

O_m i U_m— siły podłużne w przedziale m górnego i dolnego pasa,

S_m — siła poprzeczna w przedziale m pręta, Q_m— siła poprzeczna w m-tej poprzeczce,

Mm i Mm—momenty zginające w prawym i lewym końcu m-tego pola dolnego pasa,

Mm i M°_m— te same momenty dla górnego pasa.

Mbm Mb_m — momenty zginające w końcach blachy mm,

— ugięcie się osi pręta w punkcie m,

i ń — kąt nachylenia dolnego i górnego pasa w m,

a_m i — kąt obrotu dolnego i górnego końca

m-tej poprzeczki,

— kąt nachylenia przekroju m względem przekroju m—1 przy zupełnej sztywności poprzeczek.

Między powyższymi 16 wielkościami ustala Muller-Breslau potrzebną ido ich wyznaczenia

^u) Muller-Breslau, „Die neueren Methoden.,1913.

¹⁵) H. Kayser, Die Knickversteifung doppetwandiger Druckąuerschnitte, Der Eisenbau. 1913.