image 070

70 Pole bliskie anteny i jego znaczenie dla techniki antenowej

4.2 Pole w przekroju apertury a charakterystyka promieniowania

W rozdziale 3 pokazaliśmy sposób wykorzystania potencjałów wektorowych do określenia pola w strefie dalekiej. Okazuje się jednak, że możliwe jest określenie tego pola przy wykorzystaniu znajomości pola w obszarze apertury promieniującej. Na wstępie rozważymy przypadek dwuwymiarowy skupiając się na interpretacji fizycznej proponowanej reprezentacji widmowej pola. Użyteczne zależności analityczne przedstawimy dla bardziej praktycznego przypadku trójwymiarowego.

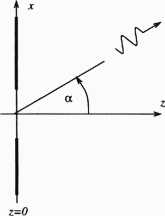
Rozważmy szczelinę w nieskończenie rozległej powierzchni idealnego przewodnika. Zakładamy przy tym, że struktura jest jednorodna względem zmien-nej y - problem rozważamy więc w przestrzeni zmniennych (x,z) (rys. 4.2) Przyjmijmy, że pole elektryczne leży w płaszczyźnie xOz i że jest sumą ele-

\AA—

Rys. 4.2. Ilustracja graficzna padania fali płaskiej na szczelinę w przewodniku i jej rozchodzenia się w półpłaszczyźnie z ^ 0 mentarnych fal płaskich rozchodzących się w prawej półpłaszczyźnie z ^ 0. Każda z tych fal ma amplitudę, ich kierunek wyznacza zaś kąt a mierzony względem osi z. Przykładowo, składowa dE_x może być zapisana w postaci:

dE_x(x, z) =    A(a)e~^^x sin'“ + ^{z cos} “) (4.19)

Już pobieżna analiza (4.19) wskazuje, że przyjęcie rzeczywistych kątów a z przedziału a G< -7r/2,7r/2 > uniemożliwia dokładne opisanie pola w półpłaszczyźnie z ^ 0. Dla opisania pola bliskiego musimy wprowadzić zespolone kąty a (rys. 4.3)

(4.20)

, ,7T    .    ,

or = ±(- +jai)