image 072

72 Pole bliskie anteny i jego znaczenie dla techniki antenowej

Funkcja k_z (patrz (4.25)) jest dwuwartościowa - wybór prawidłowego pierwiastka w (4.26) jest możliwy przy wykorzystaniu warunku wypromieniowania (rozdział 2.1). Jeśli więc k_z jest rzeczywiste, wybieramy znak (-f), gdyż gwarantuje to narastanie fazy przy wzroście zmiennej z, a więc opisujemy ruch falowy w kierunku dodatnich wartości z. W przypadku gdy k_z jest urojone, wybieramy znak minus, co oznacza malenie amplitudy pola w kierunku dodatnich wartości z.

Znajomość składowej E_x(x, z) umożliwia określenie składowej E_z(x, z) -do tego celu skorzystamy z warunku dla fali płaskiej k ■ E = 0. W efekcie uzyskujemy pole w półpłaszczyźnie z ^ 0:

E(x, ^{Z) =} Ł I⁺I⁽'^x ~ V_z    tz)F_x(k + (4.27)

Warto zauważyć, że pole w dowolnym punkcie półprzestrzeni z ^ 0 (również w strefie dalekiej), wyrażone zależnością (4.27) jest określone jednoznacznie poprzez funkcję F_x(k_x), którą nazywa się w technice antenowej widmem kątowym pola. Widmo kątowe pola można obliczyć wykorzystując fakt, że jest ono związane ze składową styczną pola w aperturze poprzez transformatę Fouriera (patrz (4.26) dla z = 0):

F_x(k_x) = P°° E(x,0)e>^k*^xdx(4.28)

J-oo

W technice antenowej zwykle interesuje nas pole w strefie dalekiej, czyli wartość asymptotyczna (4.27) przy r —> oo. Jakkolwiek można znaleźć rozwiązanie wyżej wymienionego problemu (patrz [14]), my skupimy się na bardziej praktycznym rozwiązaniu przypadku trójwymiarowego, w którym apertura promieniująca w płaszczyźnie idealnego przewodnika ma skończone rozmiary (rys. 4.4). Dla przypadku trójwymiarowego założymy, że pole w półprzestrzeni

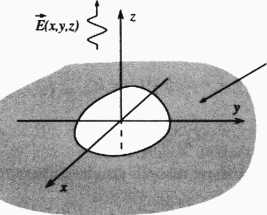
idealny

przewodnik

Rys. 4.4. Apertura promieniująca w dodatnią półprzestrzeń z ^ 0