image 071

Pole w przekroju apertury a charakterystyka promieniowania 71

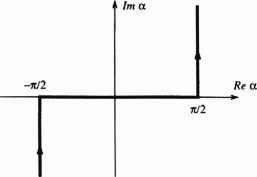
Rys. 4.3. Kontur całkowania na zespolonej płaszczyźnie kątów a umożliwiający opis pełnego pola promieniowania w półpłaszczyźnie z ^ 0

W istocie, wprowadzając (4.20) do (4.19) uzyskujemy rozwiązania w postaci:

dE_x ~ e~^kz sinh ai e^~i^kx cosh ai    (4.21)

czyli fale niejednorodne, których wpływ jest znaczący w pobliżu szczeliny (pole bliskie), a które zanikają, gdy oddalamy się od przekroju szczeliny (z —► oo). W literaturze fachowej ta część widma bywa nazywana częścią niewidzialną widma (invisible region), gdyż nie można jej zaobserwować będąc w strefie dalekiej. Fale jednorodne nazywa się częścią widzialną widma (yisible region), gdyż docierają one do strefy dalekiej (mogą być obserwowane w nieskończoności).

Aby znaleźć całkowite pole w prawej półpłaszczyźnie z ^ 0, musimy zsumować wszystkie fale, czyli dokonać całkowania wzglądem kąta a wzdłuż konturu leżącego na płaszczyźnie zespolonej, jak to przedstawiono na rys. 4.3. Takie całkowanie może być uciążliwe i z tego względu dokonamy podstawienia:

kx = k sin a kz = k cos a	(4.22)
Fx(kx) — XA(a) dkx = kd(sina)	(4.23)
W efekcie uzyskujemy:
k^2x += k^2	(4.24)
czyli
3c^H 1 (N •Ad II N	(4.25)

całkowanie dla składowej E_x w nowych granicach przyjmie zaś postać:

(4.26)

E_x(x,z) = T F_x(k_x)e-i(^k*^x + ^k‘^zUk_x