6161619712

Liczba stopni swobody cząsteczki jest równa sumie stopni swobody tworzących ją atomów. Każdy atom ma trzy stopnie swobody ruchu, odpowiadające współrzędnym kartezjańskim. Zatem cząsteczka składająca się z n atomów ma 3n stopni swobody. W przypadku cząsteczek nieliniowych trzy stopnie swobody dotyczą translacji, a trzy kolejne ruchu obrotowego. Pozostałe 3n-6 stopnie swobody opisują ruchy oscylacyjne i odpowiadające im drgania normalne. Cząsteczki liniowe mają tylko dwa rotacyjne stopnie swobody, więc ich drganiom odpowiada 3w-5 drgań normalnych. Przykładem nieliniowej drobiny jest cząsteczka wody, która składa się z trzech atomów, ma zatem 3-3 - 6 = 3 stopnie swobody oscylacyjnej. Odpowiadające im trzy drgania normalne przedstawiono na Rys. 1.

Do przybliżonego opisu oddziaływania cząsteczki dwuatomowej z promieniowaniem elektromagnetycznych wykorzystuje się model oscylatora harmonicznego. Oscylatorem harmonicznym jest w tym przypadku układ dwóch mas (atomów lub rdzeni atomowych), drgających doskonale sprężyście wokół środka masy układu. Częstość drgań własnych takiego oscylatora (v_osc) wyraża się wzorem: gdzie/to stała siłowa, będąca miarą siły wiązania, natomiast m_r oznacza masę zredukowaną, równą iloczynowi mas obu atomów podzielonemu przez ich sumę.

Energia mikrooscylatora jest kwantowana i dla poszczególnych poziomów energetycznych oscylacji wyraża się wzorem:

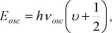
(2)

gdzie u - oscylacyjna liczba kwantowa, która może przyjąć wartości u = 0, 1, 2, 3, ...

Oddziaływanie promieniowania podczerwonego z oscylującymi cząsteczkami jest możliwe tylko wtedy, gdy spełnione są pewne warunki nazywane regułami wyboru. Zgodnie z pierwszą regułą, energia fotonu promieniowania elektromagnetycznego, która może zostać pochłonięta przez cząsteczkę musi odpowiadać różnicy energii poziomów energetycznych cząsteczki (dla spektroskopii oscylacyjnej A.E_osc = hv). W przypadku oscylatora harmonicznego dozwolone są tylko przejścia absorpcyjne lub emisyjne, dla których oscylacyjna liczba kwantowa zmienia się o Au = ±1.

Przedstawiony model oscylatora harmonicznego wyjaśnia występowanie tak zwanych pasm podstawowych, czyli intensywnych pasm absorpcyjnych w widmach cząsteczek heteroatomowych, którym towarzyszy zmiana oscylacyjnej liczby kwantowej Au = 1. W widmach obserwowane są również pasma o niskiej intensywności i o częstościach zbliżonych do wielokrotności częstości pasma podstawowego, są to tzw. nadtony. Ich występowanie wyjaśnia model oscylatora anharmonicznego. Najważniejszą konsekwencją zastosowania tego modelu jest rozszerzenie reguły wyboru dotyczącej zmiany liczby kwantowej oscylacji -dozwolone stają się przejścia, dla których oscylacyjna liczba kwantowa zmienia się o kilka jednostek (Au = ±1, ±2, ±3, ...). Warunek ten stanowi drugą regułę wyboru obowiązującą w spektroskopii w podczerwieni. Z trzeciej reguły wyboru wynika natomiast, że w podczerwieni można obserwować tylko te przejścia oscylacyjne, którym towarzyszy zmiana momentu dipolowego cząsteczki. Drgania te nazywa się drganiami aktywnymi w podczerwieni.

Rzadko obserwuje się teoretyczną liczbę drgań normalnych tonów podstawowych, ponieważ nadtony i drgania złożone, czyli suma lub różnica kilku drgań, zwiększają liczbę pasm, natomiast inne zjawiska zmniejszają ich liczbę. Gdy dwa oscylujące wiązania mają wspólny atom, pomiędzy utworzonymi oscylatorami istnieje oddziaływanie mechaniczne i z tego względu rzadko zachowują się jak odrębne oscylatory, chyba że częstości ich drgań są