673060934

gdzie cztery kolumny macierzy A odpowiadają czterem wierszom macierzy B, a w wyniku mnożenia otrzymujemy macierz C_3s5 o liczbie wierszy macierzy A i liczbie kolumn macierzy B

Niech A = [a_y], B = [by], C = [c,.] będą macierzami o wymiarach m x n. Macierz C jest sumą macierzy A i B, co zapisujemy A + B = C, wtedy i tylko wtedy, gdy wszystkie c_y = a_y + b_y, dla każdego i = 1,2, ..., m, j = 1,2,..., n.

PRZYKŁAD 1.9. Niech będą dane macierze:

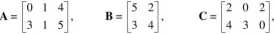
Wykonaj możliwe dodawania macierzy.

Ze względu na wymiary macierzy możliwe jest dodawanie macierzy A i C i ewentualne wielokrotne dodawanie jednakowych macierzy (na przykład B + B).

[o :	1 4l [2	0	21	[0 + 2	1+0 4 + 2]
■[3 i	15H4	3	oj	^_[3 + 4	1+3 5 + of

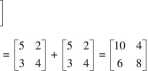
2 1 6 7 4 5

E = B + B

Druga suma jest równoważna iloczynowi liczby 2 i macierzy B. Dlatego też wygodnie jest zdefiniować iloczyn liczby rzeczywistej i macierzy. Mnożenie przez liczbę jest skróconym dodawaniem. Zamiast dodawać te same macierze, można pomnożyć ich elementy przez odpowiednią liczbę, równo liczbie dodawań. Można zapisać, że iloczynem macierzy A = [a_y] o wymiarach m x n i liczby rzeczywistej X nazywamy macierz B = £b_y], także o wymiarach m x n, której elementy są określone następująco:

b.. = X • a. dla i = 1,2,..., m, j = 1,2,..., n.

Wykonane w Przykładzie 1.9 działanie B + B jest równoważne mnożeniu macierzy B przez liczbę 2.

19