7270841635

Oryginalna f(t)	Transformata F(s)
i(»)(i-#r	n! s(.s+l)(s+2)...(.s+w)
l(/)sin(io<)	co 5^2 + C0^2
l(/)cos(co/)	s^2+co^2
l(/)e^_0'sin(cof)	(s+a)’W

Tabela 4.1: Przykładowe transformaty

4.2 Własności transformaty La place'a

1.    Liniowość:

af i(t)+bf₂(t) <=* aF_l(s)+bF₂(s)

2.    Skalowalność:

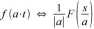
3.    Przesunięcie w czasie:

f(t-r) » F(s)e~^ST

4.    Przesunięcie w dziedzinie częstotliwości:

e~^a'f(t) « F(s+a)

5.    Splot w dziedzinie czasu:

/,(')*/«= j/iW»/₁(<-T)rfT « F,(_S)-F₂(_S)

6.    Splot w dziedzinie częstotliwości:

7.    Jednostronne różniczkowanie w dziedzinie czasu:

» »F(_S)-/(0-)

8. Jednostronne różniczkowanie w dziedzinie czasu dla zerowych warunków początkowych i dla niezerowych warunków początkowych:

id"

o _s"F(s)+y-7(oi-/^_V‘^l(o^_) ... /-"(ot

dt

4.3 Odwrotna transformata La place'a

Problem transformacji odwrotnej sprowadza się do rozwiązania równania całkowego Laplace'a:

F(s)=j/(r)e-”rfT

a poszukiwana funkcja /(/) będzie rozwiązaniem transformacji odwrotnej Laplace'a:

Podstawy sterowania 12