7292100149

(4.73)

gdzie:

o - składowa pionowa naprężenia,

E_s- moduł sprężystości,

V - objętość skały.

Energia sprężysta akumulowana w skale osiągnie wartość maksymalną, gdy a = R_c. Wówczas jednostkową energię odkształcenia sprężystego [V = 1 m³) wyraża wskaźnik PES

PES =

lOOOftg 2 Es

500 • —

Es

(4.74)

gdzie:

R_c - wytrzymałość na jednoosiowe ściskanie, MPa;

E_s - moduł sprężystości przy nawrocie odkształceń, MPa.

Na podstawie wyników badań opracowano klasyfikację skłonności skał płonnych do tąpań (rys. 4.105).

PES < 50 kJ/m^3		PES = 50-100 kJ/m^3		PES = 101-200 kJ/m^3		PES > 200 kJ/m^3
• skały nieskłonne		• skały słabo skłonne		• skały silnie skłonne		• skały bardzo silnie
do tąpań		do tąpań		do tąpań		skłonne do tąpań

Rys. 4.105. Klasyfikacja skłonności do tąpań skał płonnych, według wskaźnika PES (Smółka i in. 1978)

Kinetyczny wskaźnik tąpliwości

Filcek (1980), na podstawie pojęcia minimalnej energii kinetycznej oraz wyników doświadczeń wykonanych przez Drzewieckiego (1967), zaproponował nowe ujęcie energetycznego wskaźnika skłonności skał do tąpań w postaci kinetycznego wskaźnika tąpliwości H, określanego jako wielokrotność minimalnej jednostkowej energii kinetycznej

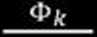
(4.75)

gdzie:

<l>A mtn - minimalna jednostkowa energia kinetyczna tąpnięcia (1,25 • 105 J/m³), <1>a    - energia kinetyczna rozpadu skały.

Wskaźnik kruchości W_Zt (wskaźnik zagrożenia tąpaniami) został określony na podstawie przedzniszczeniowej części charakterystyki naprężeń iowo--odkształceniowej jako iloraz energii właściwej (Gustkiewicz i in. 1987)

W_ZT = £    (4.76)

158