8254445087

42

i SEP, ponieważ AM:EP=L’ :L, a podstawiając 3 wiadome wielkości, otrzymujemy proporcję:    ¹/2S₀b:¹/₂Sib=L’:L, skąd L’ = —^s-5—.L

s₀ + Sj

Z podanego wzoru widzimy ,że odległość L’ jest zależną od spadków s₀ i Sj .i zawsze jest mniejsza od potowy L, gdyż s_L > s₀, a równa siię l/₂L przy s₀ = s₃, to jest wtedy, gdyby przejście od przekroju normalnego dwuspadkowego do przekroju jedno spadkowego; miało się odbywać przy jednym spadku s₀, jak w pierwszym sposobie (A).

Dla większej jasności i przejrzy stqści powyższych rozważań podaje się rys. 32, na którym' są wykreślone 4 przejściowe stad ja przekroju poprzecznego: na początku przejściowego odcinka L’, pośrodku jego i w końcu tegoż odcinka, czyli na początku łuku, wreszcie na długości L\

przekrój poprzecznii jezdni na końcu L

Na całej długości łuku pozostaje poprzeczny spadek jezdni Sj

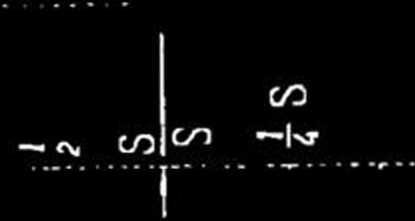
przekrój poprzecznij jezdni pośrodku L

przekrój poprzecznij jezd na dzugosci L

przekrój poprzeczni) jezd. na początku L

Rys. 32.

Zarysy tych przekrojów są następujące: AMQ, CND, EF i RSW...

Zrozumiałem jest, że pośrodku przejściowego odcinka L punkt N (na osi jezdni) winien znajdować się na pcłowie wysokości MP, zaś punkt C (na zewnętrznej krawędzi jezdni) — winien, znajdować się na połowie wysokości AE. Mając wyliczone wartości wzniesienia zewnętrznej krawędzi i osi jezdni, oraz wartości spadku wewnętrznej krawędzi jezdni (poszerzenia) łatwo już określić odpowiednie koty dla linji przejściowej i łuku, o ile zakręt przebiegałby nie w terenie poziomym, a na dowolnym spadku podłużnym, dodając, względnie odejmując od.powiędnie wartości niwelety podłużnego profilu projektowanej drogi.

Należy jeszcze rozpatrzeć załamanie się niwelety podłużnej w przekrojach AMB (rys. 30 wszględńie 31) i EPF, zwłaszcza przy drugim (B)