834706954

I numerosi esempi proposti da Frezier nel primo libro concorrono tutti allo stesso scopo: dimostrare, a partire da una curva gobba ricavata per sezioni paral-lele di superfici quadriche che si intersecano, la specie delle curve gobbe trovate (figg. 10,13).

Le ragioni della ricerca presentata nel primo libro si palesano nel secondo, in cui 1'autore si pone il problema della costruzione grafica delle quartiche, e in cui propone delle soluzioni che sussistono proprio in virtu della relazione proiettiva che lega le loro linee notevoli a quelle delle coniche da cui hanno origine.

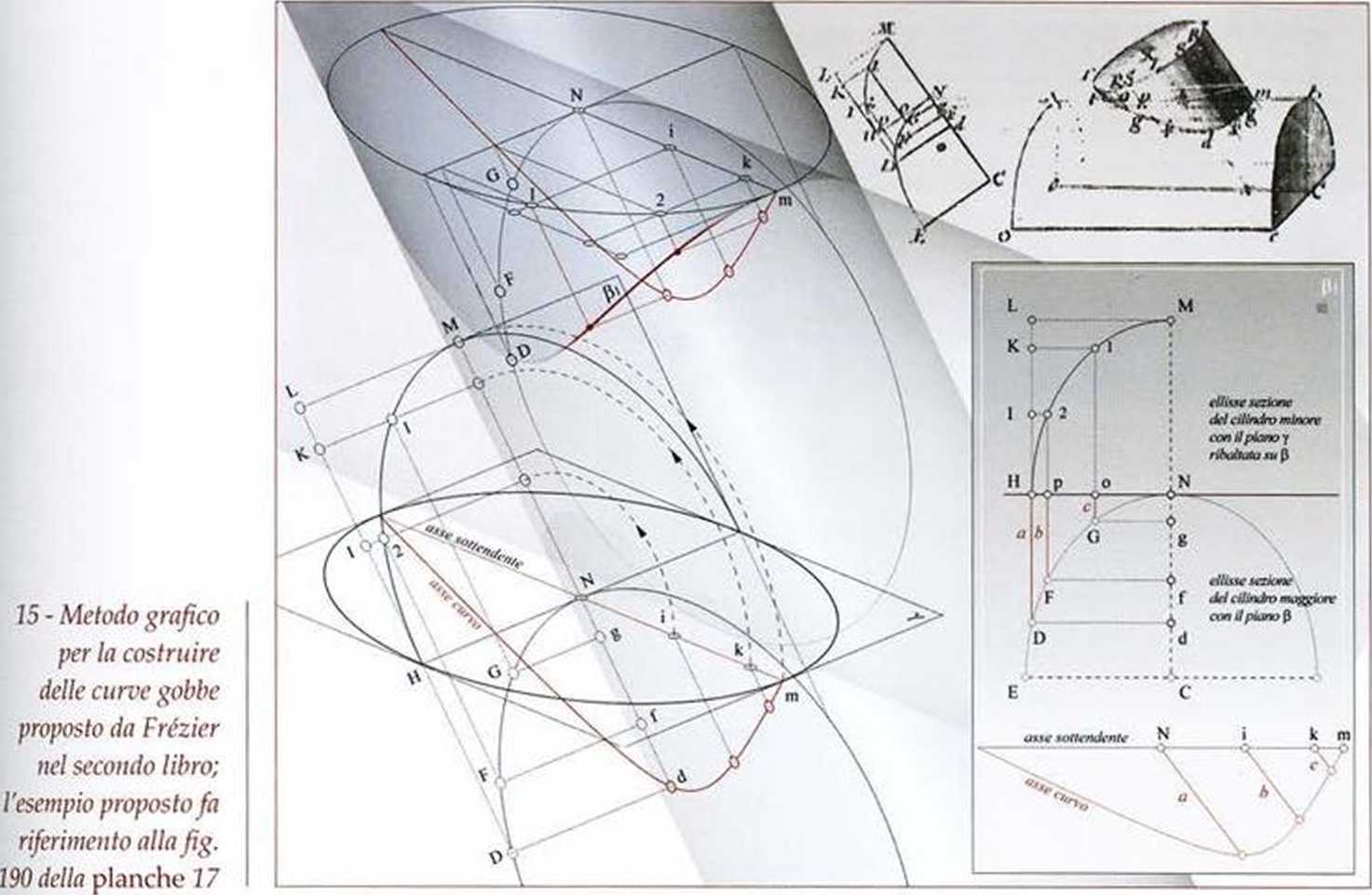
Per poter costruire le curve del quarto ordine Frezier ricerca le distanze dei punti delFrtssc sottendente della conica di base, che si immagina assegnata, da quelli corrispondenti suWassc currn. NelFesempio precedente in cui la curva e un 'ellipsimbrc, tale distanza, per la congruenza delle ord i na te, sara pari a quella che sussiste fra punti corrispondenti delFellisse sezione piana del cilindro mino-re e della curva gobba (fig. 15).

Questa operazione & graficamente descritta attraverso ii ribaltamento dell'el-lisse da cui ha origine la quartica (appartenente al piano y) sul piano che passa per il suo centro, che contiene la direzione di proiezione e che & perpendicolare al piano definito dagli assi delle quadriche (p in figura), piano che seziona il cilindro maggiore secondo un'ellisse. Si dovra dividere in un numero coiweniente di parti (tre in figura) 1'ellisse alForigine della quartica, riportare gli intervalli stabiliti (punti 1 e 2) sulla cerniera dcl ribaltamento e determinare i punti corrispondenti sulFellisse sezione del cilindro maggiore (punti G e F): le distanze fra

II molo di Amedće Franęois Frćzier nella nascita della Geometria Descrittiva 43