Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

1

Wykład 8. Zastosowania pochodnej c.d.

Pewne zastosowania pochodnej omówiliśmy w Wykładzie 7.

W tym wykładzie wykorzystujemy pochodne do wyznaczania
przebiegu funkcji i wyznaczania ekstremów.

I. Ekstrema lokalne

Definicja1. x

0

jest punktem wewnętrznym zbioru X

jeśli istnieje

taka liczba

że odcinek (x

0

-

x

0

+

Odcinek

(x

0

-

x

0

+

nazywamy otoczeniem punktu x

0

Załóżmy, że x

0

jest punktem wewnętrznym dziedziny pewnej funkcji

f.
Definicja 2.( Ekstremum lokalne). Mówimy, że funkcja f osiąga
maksimum (minimum) lokalne w x

0

jeśli takie istnieje otoczenie

(x

0

-

x

0

+

, że

f(x

0

)

f(x) (f(x

0

)

f(x)) dla x (x

0

-

x

0

+

W przypadku ostrych nierówności dla x x

0

mówimy, że funkcja ma

w punkcie x

0

maksimum (minimum) właściwe.

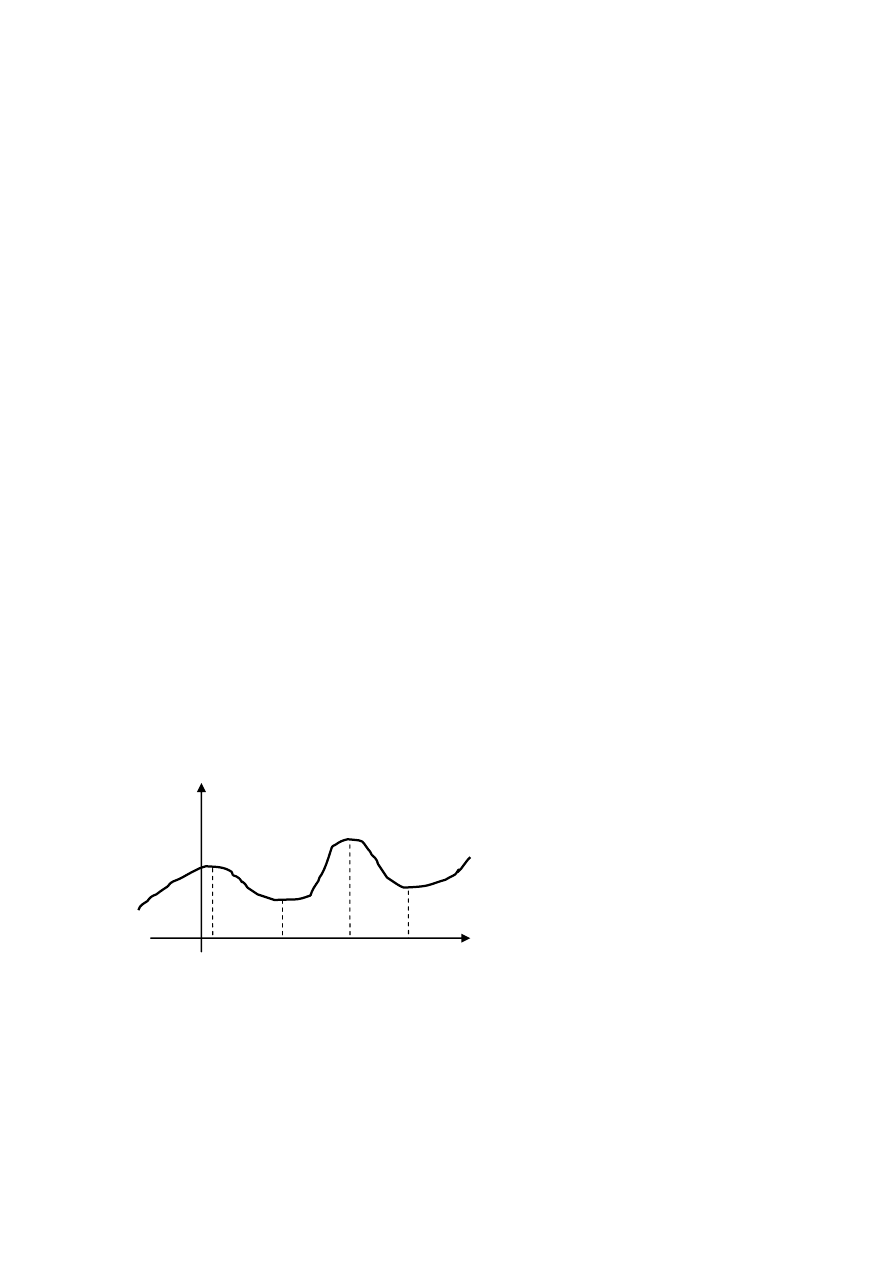
f(x)

x

1

x

2

x

3

x

4

Rys.1 W punktach x

1

, x

3

, f(x) osiąga maksimum lokalne a w

punktach x

2

, x

4

, minimum lokalne.

Definicja 3. Minima i maksima lokalne nazywają się lokalnymi
ekstremami.

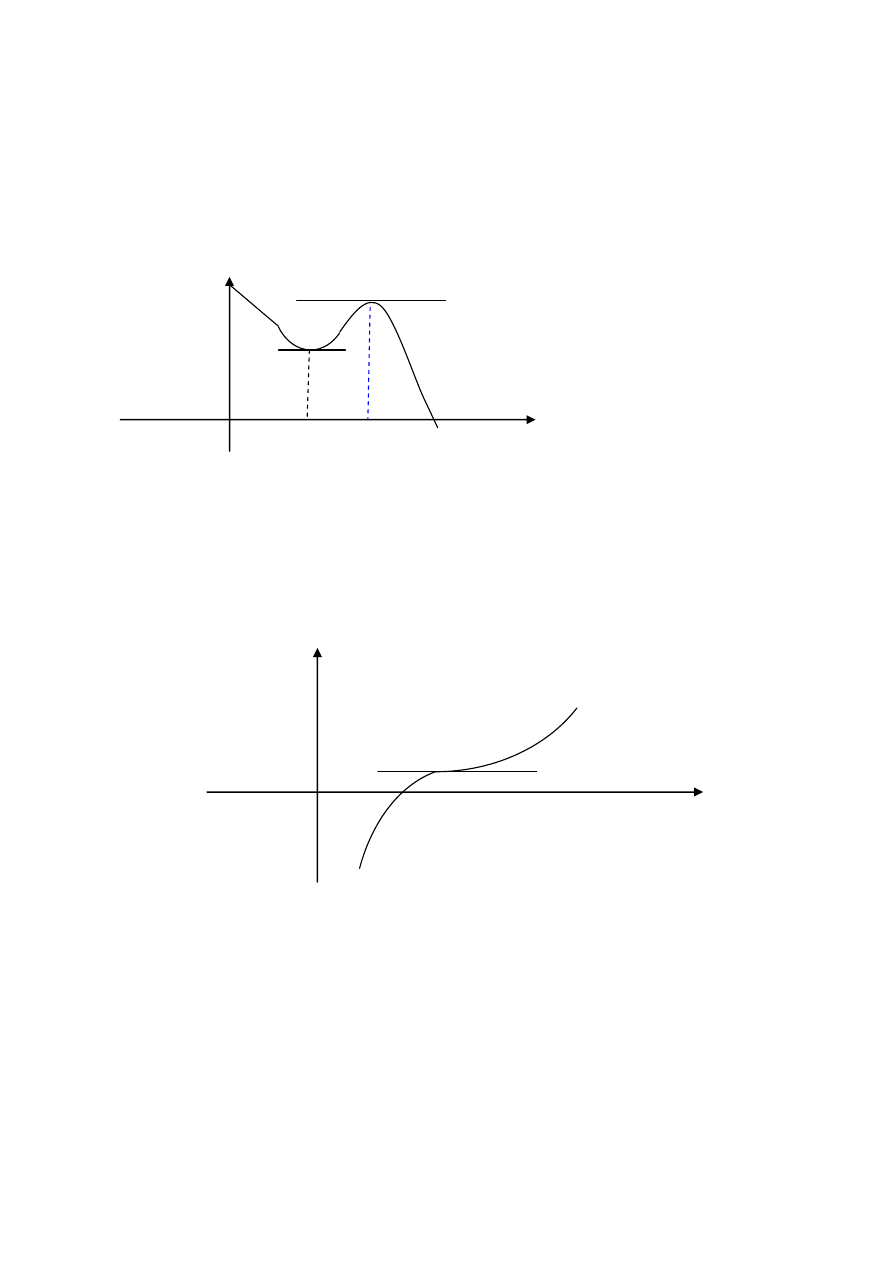
Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

2

Twierdzenie 1. (Twierdzenie Fermata. O zerowaniu pochodnej w
punkcie ekstremum). Jeżeli f ma w punkcie x

0

ekstremum i jest w

tym punkcie różniczkowalna to jej pochodna w tym punkcie jest
równa zero.

Dowód pomijamy.

f(x)




x

1

x

2

x

Rys.2 W punkcie x

1

funkcja f ma lokalne minimum,

w punkcie x

2

lokalne maksimum. W obu punktach

styczne do wykresu są równoległe do osi x. Oznacza
to, że f

( x

1

)= f

( x

2

)=0.

Uwaga. Twierdzenie odwrotne nie jest prawdziwe (por.Rys.3)

f(x)



x

1

x

Rys.3. W punkcie przegięcia x

1

styczna jest równoległa do osi x,

zatem f

(x

1

) = 0, ale to nie jest ani minimum ani też maksimum

funkcji f.

Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

3

Twierdzenie 2. (Rolle’a). Jeśli funkcja f jest ciągła w przedziale

domkniętym [a,b] i różniczkowalna w (a,b), a na końcach przedziału

przyjmuje jednakowe wartości f(a)= f(b), to istnieje w przedziale

(a,b) taki punkt c, że f (c)=0 (por. Rys 3)

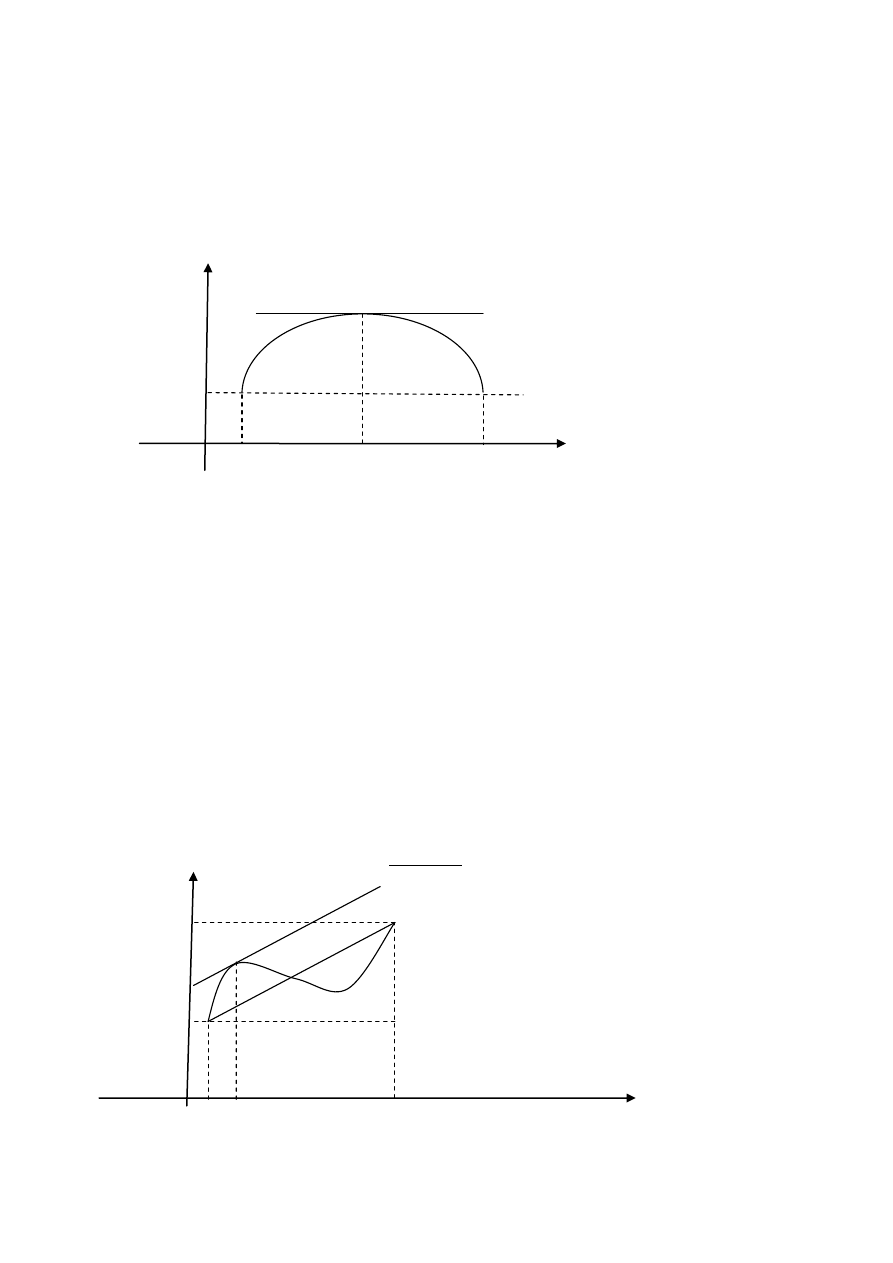
f(a)=f(b)


a c b x
Rys. 3. Styczna do wykresu funkcji f w punkcie c jest równoległa do
osi x. Oznacza to, że f

(c)=0.

Z twierdzenia Rolle’a wyprowadza się następujące twierdzenie
Lagrange’a o przyrostach.

Twierdzenie 3. ( Twierdzenie Lagrange’a o przyrostach)

Jeśli funkcja f jest ciągła w przedziale domkniętym [a,b] i

różniczkowalna w (a,b), to istnieje w przedziale (a,b) taki punkt c, że

f

(c) =

(por. Rys.4)

f(b)
Styczna do wykresu w punkcie c jest
równoległa do prostej łączącej końce
f(a) wykresu w punktach a i b.


Rys.4 a c b

Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

4

Inny zapis tezy Twierdzenia Lagrange’a : przyrost wartości funkcji

f(b) –f(a) jest równy pochodnej w punkcie pośrednim f

(c)

pomnożonej przez przyrost argumentów: f(b) –f(a) = f (c) (b-a).

Twierdzenie 4. (Własności funkcji z ustalonymi znakami

pochodnej w przedziale)

a) Jeżeli pochodna funkcji w każdym punkcie przedziału (a,b) jest

równa zero, to funkcja w tym przedziale jest stała.

b) Jeżeli pochodna funkcji w każdym punkcie przedziału (a,b) jest

dodatnia (ujemna), to funkcja jest w tym przedziale rosnąca

(malejąca).

c) Jeżeli funkcja różniczkowalna w pewnym przedziale jest w tym
przedziale stała to pochodna jest w tym przedziale równa zero.


d) Jeżeli funkcja różniczkowalna w pewnym przedziale jest w tym
przedziale niemalejąca (nierosnąca) to pochodna jest w tym
przedziale nieujemna (niedodatnia).

Dowody punktów a)-d) opierają się na Twierdzeniu Lagrange’a.
Dla przykładu podamy dowód punktu a)

Gdyby f nie była funkcja stałą to istniałby takie dwa punkty w

przedzale (a,b), że x

1

<x

2

i f(x

1

)

f(x

2

). Zatem na mocy Twierdzenia

Lagrange’a istniałby punkt pośredni x

0

(x

1

, x

2

), że

f

(x

0

) =

, co zaprzecza zerowaniu pochodnej w (a.b)

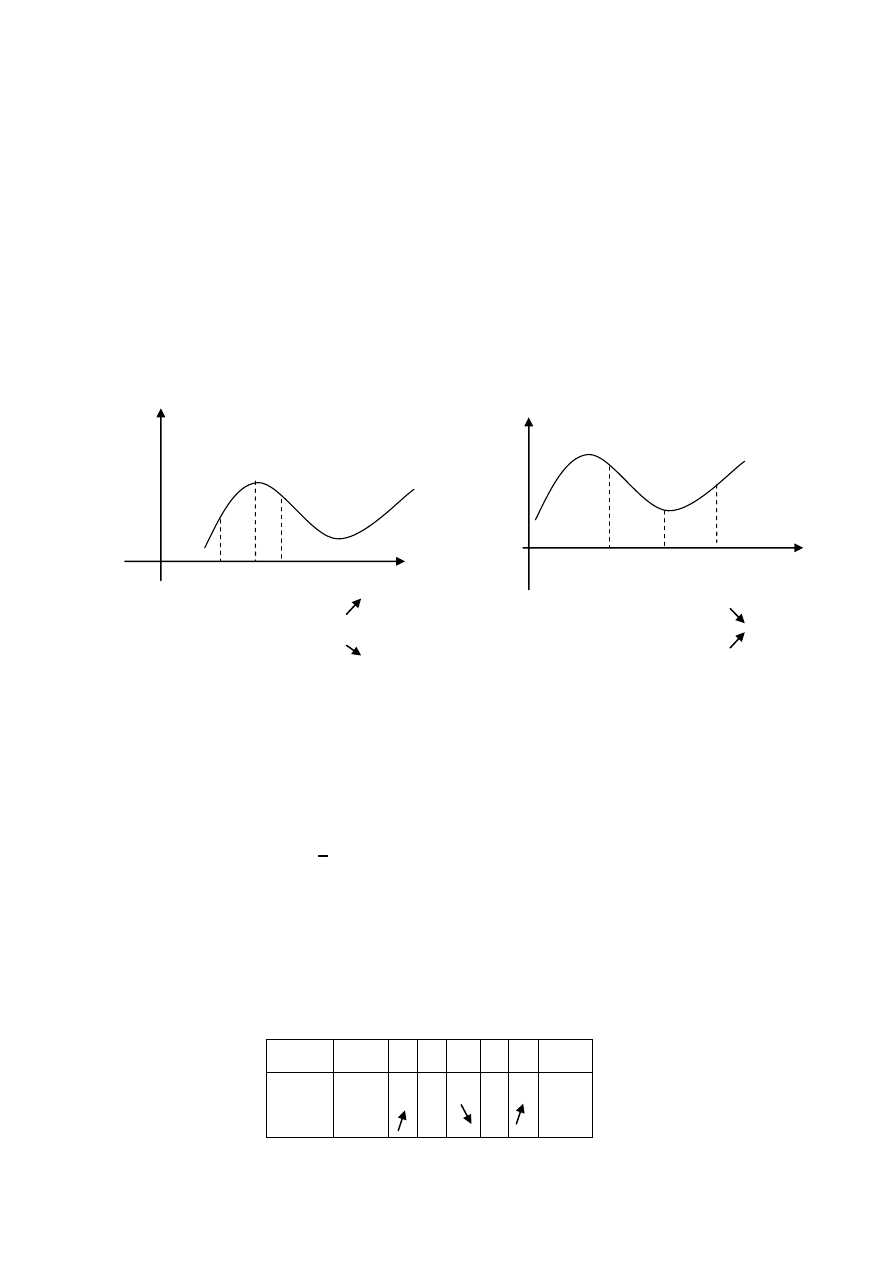
Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

5

Wniosek. Jeżeli istnie takie

, że funkcja f

- w przedziale (x

0

x

0

) ma pochodną dodatnią (ujemną),

-w punkcie x

0

ma

pochodną równą zero ( f (x

0

) = 0)

- w przedziale (x

0

, x

0

) ma pochodną ujemną (dodatnią),

to funkcja f ma w punkcie x

0

lokalne maksimum właściwe (lokalne

minimum właściwe).

f(x

0

)-

maksimum

f(x

0

)-

minimum

x

0

x

0

x

0

x

0

x

0

x

0

Rys 5.

W (x

0

x

0

): f

>0, f W (x

0

x

0

): f < 0, f

W (x

0

x

0

): f < 0, f W (x

0

x

0

): f

>0, f

W x

0

f

( x

0

) = 0 W x

0

f

( x

0

) = 0

II. Ekstrema funkcji. Wyznaczanie przedziałów monotoniczności

Zadanie. Wyznacz przedziały monotoniczności i ekstrema funkcji

f(x) =

Rozwiązanie. Wyznaczamy punkty stacjonarne (takie, w których
pochodna zeruje się).
f

(x)=

= (x-3)(x-5)

Dalsze rozumowanie przedstawia tabelka

x

3

5

f

f(x)

+

0

0 +

Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

6

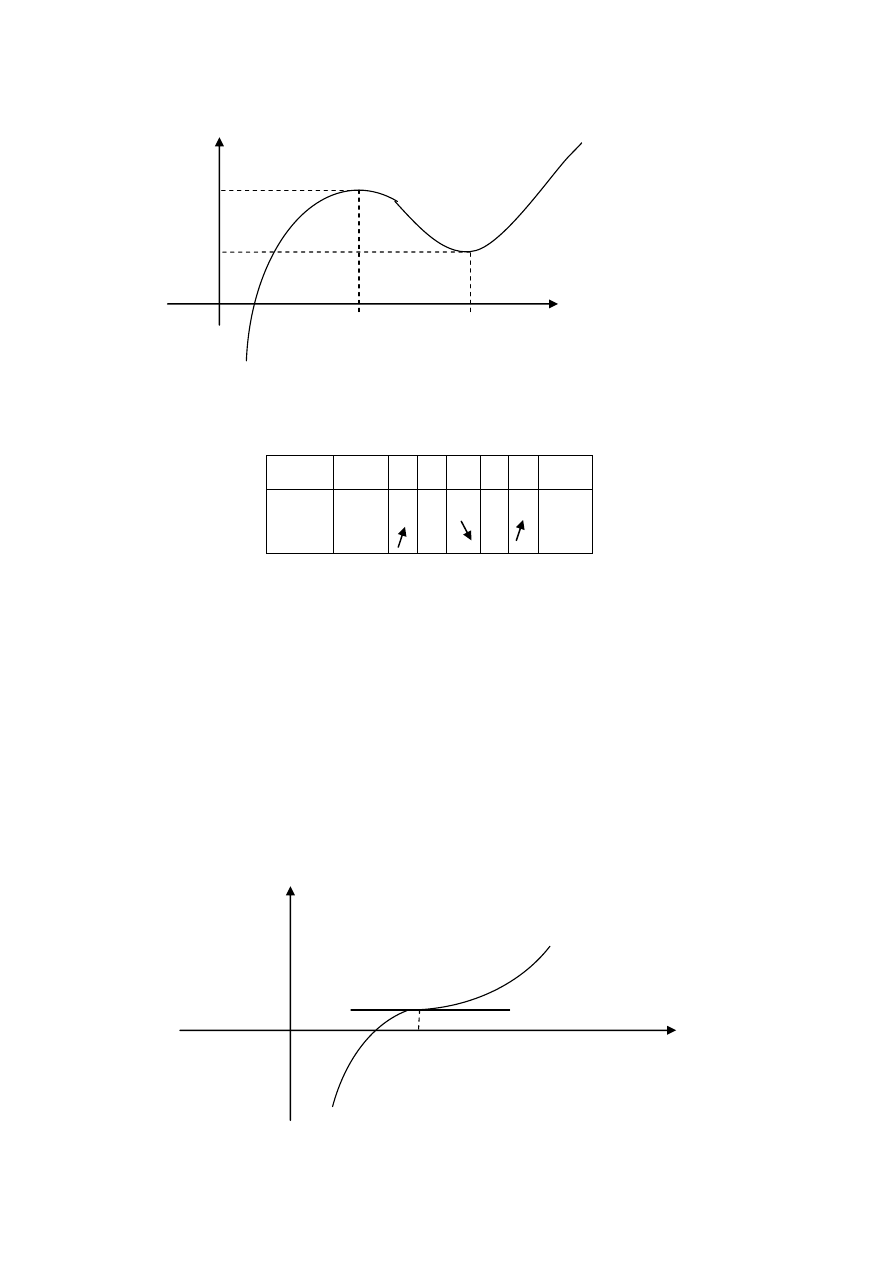
Szkic przebiegu zmienności funkcji f

3

5/3


3 5
Rys.6 Opis tego przebiegu daje poniższa tabelka

x

3

5

f

f(x)

+

0

0 +

Ekstrema lokalne:

f

max

= f(3) = 3, f

min

= f(5)=5/3

Twierdzenie 5. (Warunki wykluczające ekstremum)
Jeżeli f (x

0

)= 0, ale f

jest tego samego znaku w przedziałach

(x

0

x

0

)

i (x

0

x

0

) dla pewnego

to funkcja f jest monotoniczna w

otoczeniu x

0

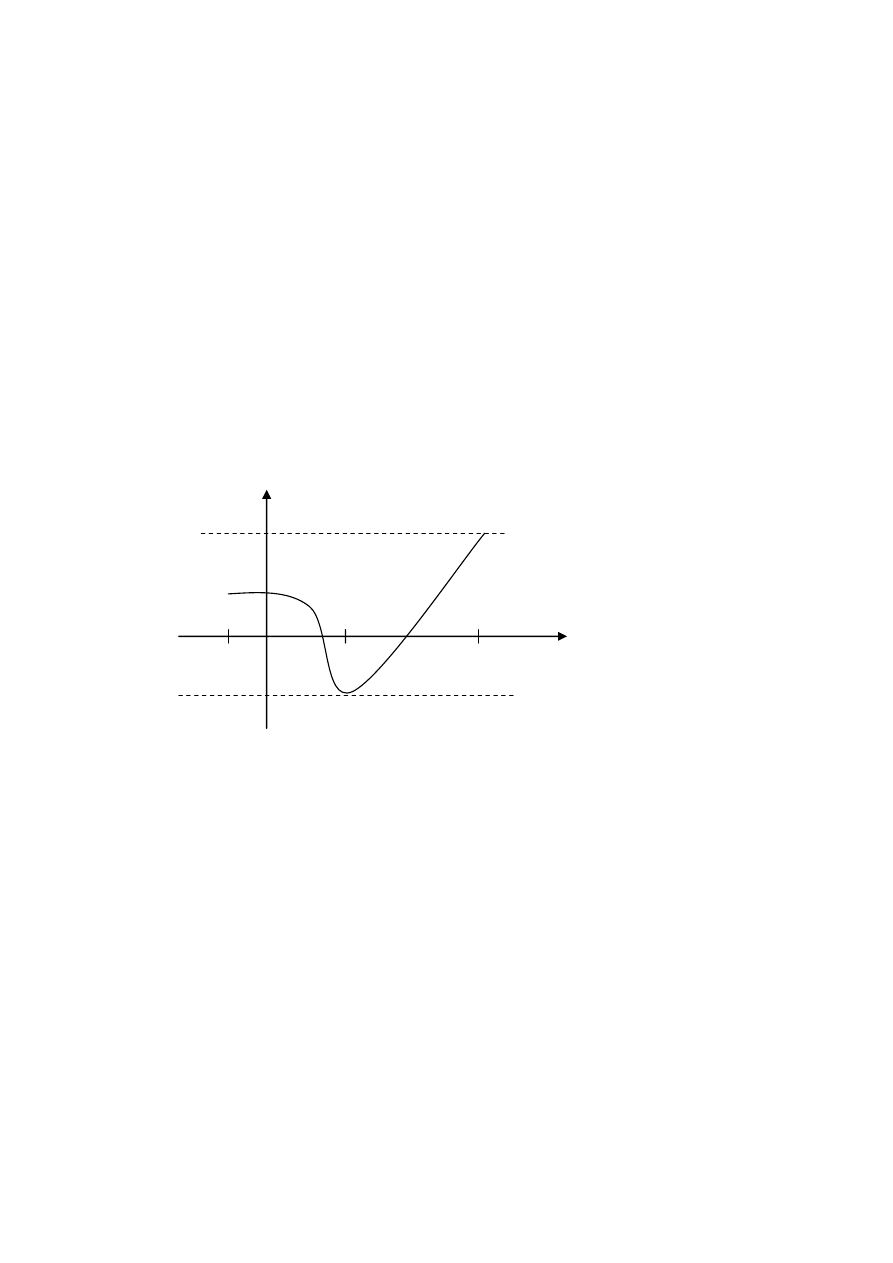
. Ilustrujemy to powtarzając Rys.3.

f(x)

Rys. 7. Przykład funkcji rosnącej, której pochodna zeruje się w x

0

x

0

Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

7

Twierdzenie 6. (Osiąganie kresów)
Jeżeli f jest ciągła w przedziale domkniętym [a,b], to istnieją w tym
przedziale takie punkty x

1

,x

2

, że

a) f(x

1

)

f(x) dla x [a,b],

b) f(x

2

)

f(x) dla x [a,b].

(Dowód pomijamy)

Komentarz. Liczbę f(x

1

) nazywamy wartością największą w

przedziale [a,b] i mówimy, ze funkcja w punkcie x

1

osiąga swój kres

górny, natomiast liczbę f(x

2

) nazywamy wartością najmniejszą w

przedziale [a,b] i mówimy, że funkcja w punkcie x

2

osiąga swój kres

dolny.
f(x

1

)

a x

2

x

1

= b

f(x

2

)

Rys. W przedziale [a,b]:wartość największa f(x

1

), wartość

najmniejsza f(x

2

).

Ekstrema globalne: największą i najmniejsza wartość funkcji.



Praktyczny sposób wyznaczania kresów funkcji ciągłej w
przedziale [a,b] i różniczkowalnej w (a,b): wyznaczyć
wartości funkcji w punktach stacjonarnych (punktach zerowania
pochodnej) oraz w punktach końcowych przedziału. W zbiorze
otrzymanych wartości wybrać największą i najmniejszą.

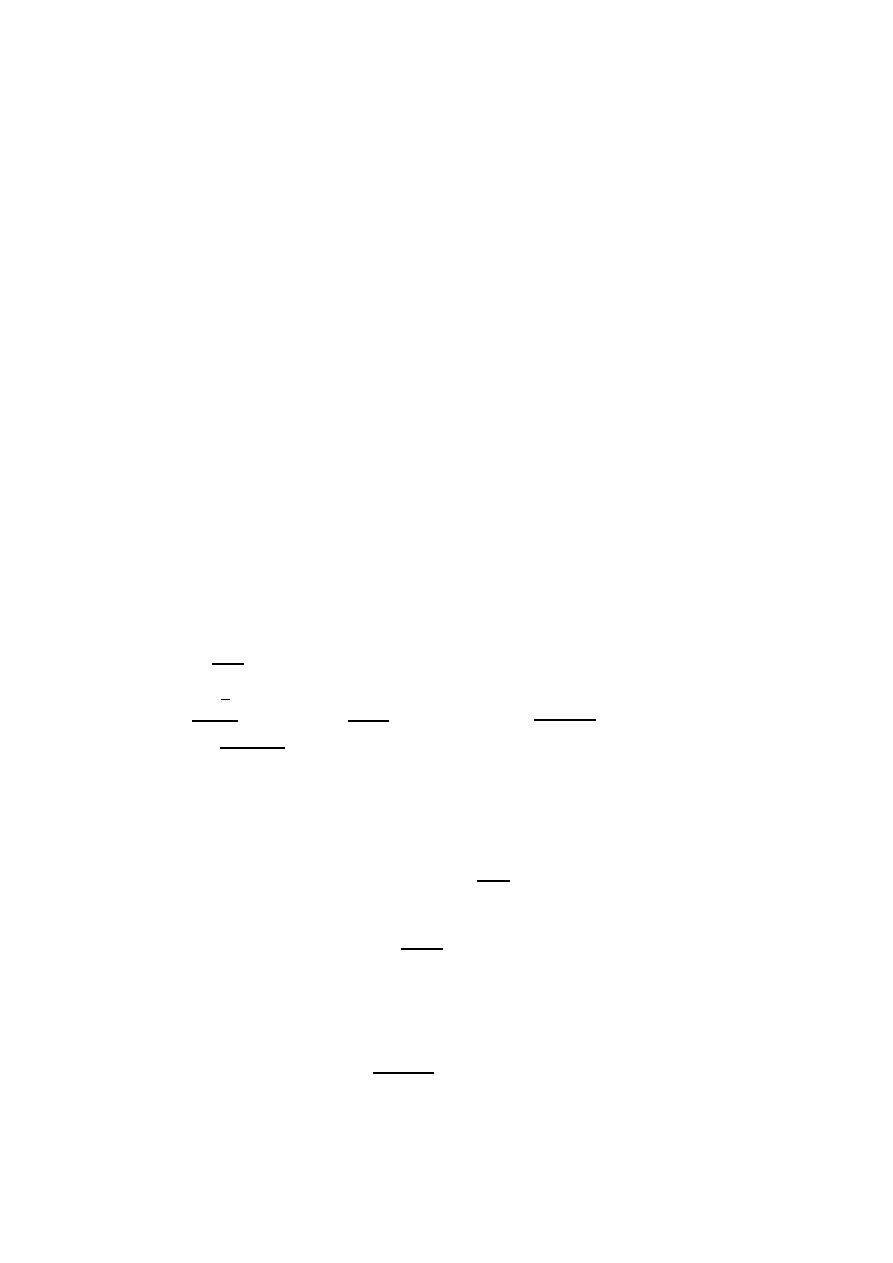
Zastosowania matematyki w ekonomii 2014. Wykład 8. R.Rempała

8

Zadanie. Wyznaczyć wartość największą i najmniejszą funkcji
f(x) =x(x-2)

2

w przedziale [-1,2]

Rozwiazanie
a) Obliczamy pochodną i wyznaczamy jej punkty zerowe.

f

(x)= (x-2)

2

+2x(x-2)=(x-2)(x-2+2x)=(x-2)(3x-2)

Punkty zerowania się pochodnej: 2 , 2/3.

Należy więc wyznaczyć max{f(-1),f(2/3),f(2)} oraz
min{f(-1),f(2/3),f(2)}.
Wyznaczając wartości w poszczególnych punktach mamy
f(-1) = -1, f(2/3)=(2/3)(4/3)

2

=32/27, f(2)=0

Wniosek.
Wartość najmniejsza w przedziale [-1,2], to -1
Wartość największa w przedziale[-1,2], to 32/27.

Zadania
1. Oblicz pochodną funkcji
a) f(x) = x

2

+3x, f(x) = x

3

+2x

2

-5x+2

b) f(x) =

f(x) = 5x

2

sinx, f(x) = 2x

2

+ cos x,

c) f(x) =

, f(x) =

, f(x) =

d)

f(x) =

, f(x) = sin

2

x f(x) = cos(1+x

2

)

2. Wyznacz dziedzinę funkcji f(x) = x+(1/x). Zbadaj czy równanie
f

ma rozwiązanie.

3.Wyznacz styczną do wykresu f(x) =

w punkcie x

0

=2.

4. Wyznacz przedziały monotoniczności funkcji:
f(x) = x

2

2x +5, f(x) =

5. Wyznacz ekstrema lokalne funkcji
f(x) =

x

2

4x , f(x) = x

2

6x , f(x) = x/(1+x

2

)

6. Załóżmy, ze cena (p) pewnego produktu zależy od popytu (x)
w następujący sposób:

; x

. Przy jakiej cenie popyt jest

największy?